First, try these challenging GMAT practice problems. Give yourself a strict time-limit of six minutes for the set.
1) If A is a number, which of the following must be true for any A?
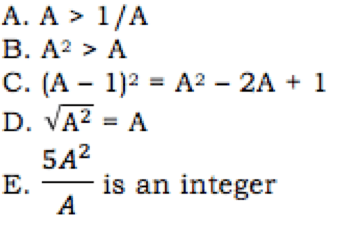
2) If F and G are integers, with F < G, which of the following must be true?
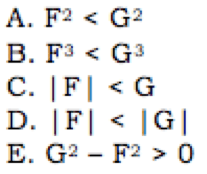
3) If J is an integer, which of the following must be true?
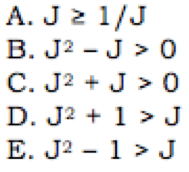
4) If p and q are two different odd prime numbers, such that p < q, then which of the following must be true?

Attacking “must be true” problems
For many math problems, one has to focus on finding the one right answer. That approach, with these problems, is highly problematic. If you are super-talented with math, fluent in Algebra, then perhaps you can scan the list of choices and immediately spot the correct answer. If you are talented enough to do that, then good for you!
For most folks, that approach is simply not feasible. The much more efficient solution involves elimination. You see, if any statement “must be true”, then it will be true for any value you pick. It takes incredible skill (or fantastic luck) to pick a single value that eliminates four answer choices and leaves only one. If that happens by chance, great, but don’t focus on that. Focus on speed and efficiency. Pick one value, eliminate what you can, then pick another, eliminate more, etc. Whittle down the choices until you are left with one. That’s the most efficient approach for these problems.
You have to pick values to plug in. At the start of picking, pick very easy values — with a few easy choices, you should be able to eliminate two or three answer choices, making your overall job much easier.
What values to pick?
If you picked the same values for all four questions above, that’s a problem. Those questions were specifically written so that the allowable numbers would be different in different questions.
When you hear “A is a number”, of what do you think? Remember that the general word “number”, like the general term “human being”, includes all types. Just as the individuals under the term “human being” constitute a bewildering variety, so do the citizens of the realm of “numbers.” Numbers include positive & negative, wholes & fractions & decimals, square-roots, pi, etc. etc. It’s a realm of perfect democracy — for example, -(pi)/5 is just as much a number as is 8. If, when a GMAT problem says “number”, your mind defaults to {1, 2, 3, 4, ..}, the “counting numbers”, then with all due respect, that’s really a third-grade way of thinking about the word “numbers”, and the GMAT will viciously punish that kind of thinking. You always must be aware of all possibilities for any category.
numbers = everything, positive/negative, zero, fractions, decimals, everything on the continuous infinity of the number line.
integers = positive and negative whole numbers = { … -3, -2, -1, 0, 1, 2, 3, …}
positive integers = the counting numbers, 1, 2, 3, 4, ..}; this list does NOT include zero, because zero is neither positive nor negative.
Remember that “odd integers” includes both positive and negatives, and “even integers” includes positives & zero & negatives. Prime numbers are, by definition, a subset of positive integers. There are no negative primes, and neither zero nor one is a prime number. It’s a very good idea to have the first few prime numbers memorized:
Primes = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …)
Notice that 2 is the only even prime number (all other even numbers are divisible by 2, and hence are not prime). After 2, the primes are an irregularly spaced set of odd numbers that continues to infinity. In fact, let’s talk a moment about their pattern
The pattern of prime numbers
In this section, I am going to dip into very advanced math, far far beyond the GMAT realm. In modern mathematics, most work around the “pattern of prime numbers” revolves around the Riemann Hypothesis, the single hardest un-answered question in all of mathematics. The great mathematician Bernhard Riemann proposed this grand question as a conjecture in an 1859 paper, and it has utterly baffled the most brilliant mathematical minds on the planet every since. Forget about answering the question — you need close to a Ph.D. in mathematics just to understand what the question is asking and what it has to do with prime numbers! (A brief graph of the central player of the Riemann Hypothesis, the Riemann Zeta Function, is shown below.)
All of which is a long-winded way of saying: there is no easy algebraic formula that always produces prime numbers. A simple pattern for prime numbers absolutely does not exist. Thus, in a “must be true” question, any answer of the form “[simple algebra expression] is a prime number” cannot possibly be true all the time. That absolutely has to be a wrong answer.
Summary
If you had any big “aha!” while reading this article, you may want to give those problems another glance before reading the solutions below. If you have any further questions or observations, please let us know in the comments section below.
Practice problem explanations
1) First of all, notice that A is a “number” — could be positive or negative or zero, whole or fraction or negative. Let’s first try a very easy choice: A = 0. Then, for the five answer choices, we get:
(A) undefined
(B) false
(C) true
(D) true
(E) undefined
Remember, if some choice leads to an “undefined” value, a divide-by-zero error, then it is not “true” for that value. Error is just as good as false for eliminating answers. We are down to (C) & (D). Try another relatively simple choice, A = -2.
(C) 1 = 1, true
(D) +2 ≠ -2, false
Remember that if A is negative, a negative squared is a positive, and the square-root sign always has a positive output. Therefore, the left side of the (D) equation is always positive, and can’t be true if A is negative.
Answer = (C).
2) For this problem, both F & G are integers — they could be positive or negative or zero, but they must be whole numbers. Here’s a suggestion — one good choice would be to pick a positive number with smaller absolute value and a negative number with a larger absolute value: say, F = -4 and G = 1. Let’s true those in the answers:
(A) 16 < 1 false
(B) -64 < 1 true
(C) 4 < 1 false
(D) 4 < 1 false
(E) 1-16 = -15 > 0 false
With one magical choice, we were able to eliminate four answer choices. Keep in mind, the combination small positive/big negative is a good one, and so is pairing a negative number with 0 (e.g. F = -4, G = 0), because zero is greater than any negative number.
Answer = (B)
3) Here, J is an integer, so it can be positive or negative or zero, but not a fraction or a decimal. Zero is always a special case among integers, so let’s start there. J = 0: then,
(A) undefined error
(B) 0 > 0 false
(C) 0 > 0 false
(D) 1 > 0 true
(E) -1 > 0 false
Here, the special case was enough to eliminate four answers. Again, remember, if some choice leads to an “undefined” value, a divide-by-zero error, then it is not “true” for that value. Error is just as good as false for eliminating answers.
Answer = (D)
4) Here, p and q are odd prime numbers. First of all, eliminate (A), because there’s no simple algebraic rule that generates prime numbers. The easiest choices for numbers are p = 3 and q = 5. Try this:
(B) 3 + 5 = 8 is divisible by 4 — true
(C) 5 – 3 = 2 is not divisible by 4 — false
(D) 5 + 3 + 1 = 9 = (5^2) – (4^2) — true
(E) (3^2) + (5^2) = 34
This last number requires comment. Every odd number is the difference between two perfect squares, because adjacent squares 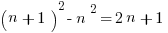 . When we subtract two even squares or two odd squares, the number is always divisible by 4. Thus, 34 cannot be the difference of any pair of squares. Thus, on the basis of this choice, we can eliminate (E). We are left with (B) & (D).
. When we subtract two even squares or two odd squares, the number is always divisible by 4. Thus, 34 cannot be the difference of any pair of squares. Thus, on the basis of this choice, we can eliminate (E). We are left with (B) & (D).
Try p = 3 and q = 7.
(B) 3 + 7 = 10 is not divisible by 4 — false
(D) 3 + 7 + 1 = (6^2) – (5^2) — true
In fact, since p & q are both odd, (p + q + 1) must be odd, and as stated above, any odd number is the difference of two perfect squares. That’s why (D) must be true.
Answer = (D)






Leave a Reply