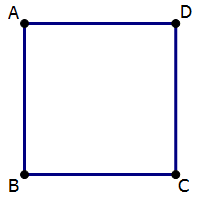
1) In quadrilateral ABCD, is angle D ≤ 100 degrees?
Statement #1: AB = BC
Statement #2: angle A = angle B = angle C
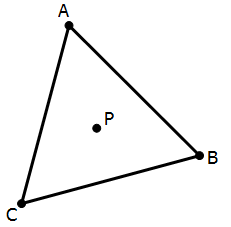
2) Point P is a point inside triangle ABC. Is triangle ABC equilateral?
Statement #1: Point P is equidistant from the three vertices A, B, and C.
Statement #2: Triangle ABC has two different lines of symmetry that pass through point P.
3) ABC is an equilateral triangle, and point D is the midpoint of side BC. A is also a point on circle with radius r = 3. What is the area of the triangle?
Statement #1: The line that passes through A and D also passes through the center of the circle.
Statement #2: Including point A, the triangle intersects the circle at exactly four points.
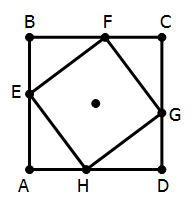
4) ABCD is a square, and EFGH is a square, each vertex of which is on a side of ABCD. What is the ratio of the area of square EFGH to the area of square ABCD?
Statement #1: AE:AB = 4:7
Statement #2: The ratio of the area of triangle AHE to the area of square EFGH is 0.24
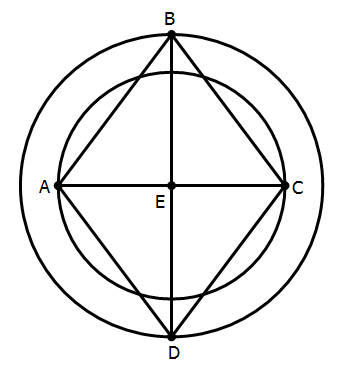
5) In the diagram above, the four triangles ABE, CBE, ADE, and CDE are all equal, and CD = 5. What is the area between the two circles?
Statement #1: AE = 3
Statement #2: angle BEC = 90 degrees

6) In trapezoid JKLM, KL//JM, and JK = LM = 5. What is the area of this trapezoid?
Statement #1: KL = 10 and JM = 15
Statement #2: angle J = 60 degrees
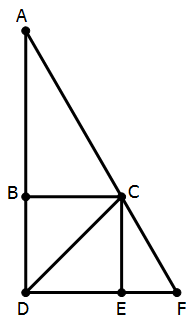
7) In the diagram above, ADF is a right triangle. BCED is a square with an area of 12. What is the area of triangle ADF?
Statement #1: angle DCF = 75 degrees
Statement #2: AB:EF = 3
8) FGHJ is a rectangle, such that FJ = 40 and FJ > FG. Point M is the midpoint of FJ, and a Circle C is constructed such that M is the center and FJ is the diameter. Circle C intersects the top side of the rectangle, GH, at two separate points. Point P is located on side GH. What is the area of triangle FJP?
Statement #1: One of the two intersections of Circle C with side GH is point P, one vertex of the triangle FJP.
Statement #2: One of the two intersections of Circle C with side GH is point R, such that RH = 7
9) Points A, B, and C are points on a circle with a radius of 6. Point D is the midpoint of side AC. What is the area of triangle ABC?
Statement #1: Segment BD passes through the center of the circle.
Statement #2: Arc AB has a length of 4(pi)
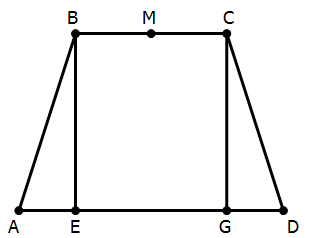
10) In the figure, ABCD is a trapezoid with BC//AD, AB = CD, BE//CG, and angle AEB = 90°. Point M is the midpoint of side BC. Point F, not shown, is a vertex on triangle EFG such that EF = FG. Is point F inside the trapezoid?
Statement #1: BE = EG
Statement #2: FG//CD
Full solutions will come at the end of this article.
Geometry on the GMAT Data Sufficiency
Here are two previous blogs on GMAT DS questions about Geometry.
GMAT Data Sufficiency: Congruence Rules
GMAT Geometry: Is It a Square?
One big difference between Geometry on the PS questions and Geometry on the DS questions is that for all the PS questions, unless otherwise noted, you know that all diagrams are drawn as accurately as possible. That is the written guarantee of the test writers. By contrast, no guarantee at all accompanies the diagrams on the DS questions. Consider the following diagram.
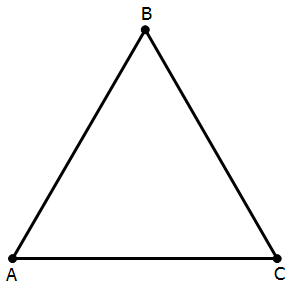
This triangle appears equilateral. There is no guarantee that it is exactly equilateral, with three exactly equal sides and angles exactly equal to 60 degrees. If this were diagram given on a PS questions, we would know that the triangle is at least close to equilateral: all the side lengths are close to one another, and the angles are close to 60 degrees. We would know that much on a PS question. If this diagram were given on a DS question, then triangle ABC could be absolutely any triangle on the face of the Earth. It could be a right triangle, or a triangle with a big obtuse angle, or a tall & thin triangle, or a short & wide triangle, or etc. It could be any triangle at all. Aside from the bare fact that ABC is some kind of triangle, we can deduce nothing from the diagram on a DS question. Other than the bare facts of what’s connected to what, you can deduce nothing about lengths, angles, and shapes of figures given on DS questions. They may be 100% accurate or they may look nothing like the the shape described by the two statements.
Because of this, some DS questions are a real test of your capacity for spatial reasoning and geometric imagination. Many DS Geometry questions, including ones here, test your capacity to imagine how different the spatial scenario might be.
If this is not a natural gift for you, I strong recommend drawing out shapes on paper. Even get a ruler, compass, and protractor, and practice constructing specific shapes. Use straws or some other straight items to construct triangles in which you can adjust the sides and the angles. Strive to visualize and picture physically every rule of geometry you learn. By working with shapes you can see, and working with your hands, you will be engaging multiple parts of your brain that will give you a much deeper understanding of geometry.
Summary
If the above discussion gave you some insights, you may want to look back at those practice problems before jumping into the explanations below. If you don’t understand something said in an explanation here, draw it yourself, and explore the different possibilities within the constraints. The point of geometry is to see.
Text Explanations
1) The figure is drawn as a square, but on GMAT DS, there’s no reason to assume the figure is drawn anywhere to scale.
If both statements are true, then the figure could be a square, in which the answer to the prompt question would be “yes,” or it could be this figure:
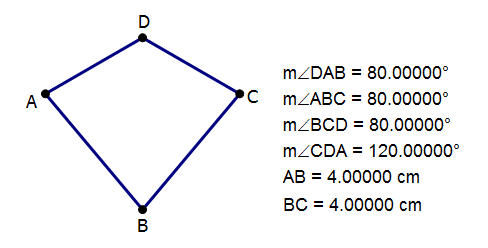
For this figure, all the conditions are met, and angle D is considerably larger than 100°; thus, the answer to the prompt question is “no.”
We could get either a “yes” or a “no” to the prompt consistent with these conditions, even with both statements put together.
Answer = (E)
2) Statement #1: As it turns out, for any triangle of any shape, there is some point that is equidistant from all three vertices: this is center of the circle that passes through all three vertices.
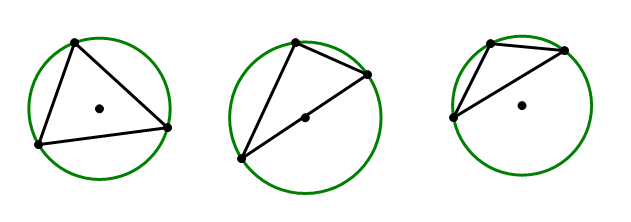
If all three angles of the triangle are acute, then the point is inside the triangle. If the triangle is a right triangle, then this center is always the midpoint of the hypotenuse. If the triangle has an obtuse angle, then the center is outside the triangle. All Statement #1 tells us is that triangle ABD has three acute angles. Beyond that, we know nothing. Statement #1, alone and by itself, is not sufficient.
Statement #2: A triangle that has a line of symmetry is isosceles. Let’s say that one line of symmetry goes through vertex A and point P. This would mean that AB = AC and that angle B = angle C. Now, let’s say that another line of symmetry goes through vertex B and point B. This would mean that AB = BC and angle A = angle C. Putting those together, we get three equal angles and three equal sides: an equilateral triangle. If a triangle has two separate lines of symmetry, it must be an equilateral triangle. We can give a definitive “yes” to the prompt question on the basis of this statement. Statement #2, alone and by itself, is sufficient.
Answer = (B)
3) Statement #1 tells us that the center of the circle is on the line of symmetry of the triangle through point A, but the triangle could be any size. In the diagram below, this line of symmetry is blue, and triangles of four different sizes are shown.
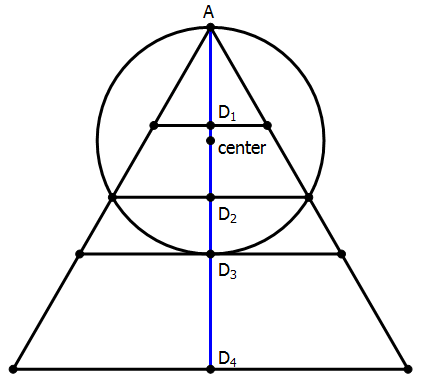
There actually would be an infinite number of possible triangle sizes on the basis of this statement alone. This statement is wildly insufficient.
Forget about Statement #1. With Statement #2 alone, a variety of off-center triangles with four intersection points are possible:
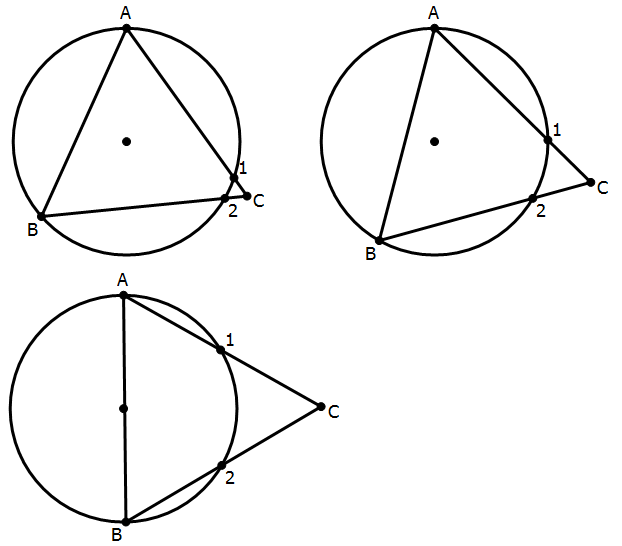
Notice AB is a chord of the circle as well as a side of the triangle. This chord could be a medium length chord or anything up to the full diameter, and different sides of the triangle would result in different areas. We still cannot give a definitive answer to the prompt question. This statement, alone and by itself, is insufficient.
Combined statements. If the center of the circle is on the line of symmetry of the triangle, then this places significant constraints on the number of intersections. For tiny triangles, they would simply intersect at point A and not reach the circle on the other side: one point of intersection, so this doesn’t work.
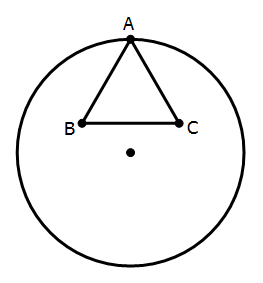
Larger triangles would touch the circle in three places, at the three vertices: this also doesn’t work.
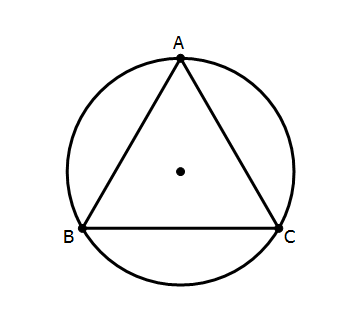
Slightly larger, and those two vertices at B and C would “poke out” of the triangle, producing five points of intersection: Point A plus four other points.
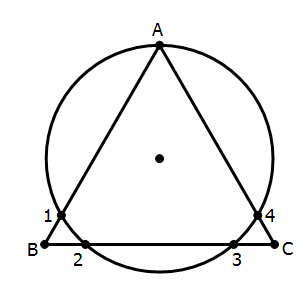
The only way we will get exactly four points is when the sides get long enough and the side BC drops low enough that it is tangent to the circle.
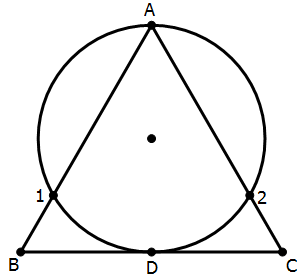
The altitude of this triangle, AD is exactly equal to the diameter. We could use the ratios of the 30-60-90 triangle to figure out the sides, and thus figure out the area. If the sides get any longer, then side BC would break contact with the circle, and there would be only three points of intersection. This triangle, with the point of tangency at D, is the only triangle on this line of symmetry that has exactly four intersection points, and we can compute its area.
The combined statements allow us to give a numerical answer to the prompt question, so together, the statements are sufficient.
Answer = (C)
4) Statement #1: since we care only about ratios, we can set any lengths that are convenient. Let AE = 4 and AB = 7: then BE = 3. The figure is symmetrical on all four sides, so, for example, AH = 3. This means AEH is a right triangle with legs of 3 and 4—that is, a 3-4-5 triangle! The hypotenuse HE = 5. That’s the side of the smaller square, and 7 is the side of the larger square. The ratio of areas is 25/49. This statement leads directly to a numerical answer to the prompt question. This statement, alone and by itself, is sufficient.
Now, forget all about statement #1.
Statement #2: triangle to small square = 0.24 = 24/100 = 6/25. Let’s say that the central square has an area of 25 and one triangle has an area of 6. This means that four triangles together would have an area of 24. The big square equals the central square plus four triangles: 24 + 25 = 49. The ratio of the two squares = 25/49. This statement also leads directly to a numerical answer to the prompt question. This statement, alone and by itself, is sufficient.
Each statement sufficient on its own. Answer = (D)
5) Statement #1: If AE = 3, then it must be true that EC = 3, because the triangles are all equal. Also, AB = BC = CD = AD = 5. Because the four angles meeting at point E are all equal, it must be true that each one equals 90 degrees. Thus, we have four right triangles, and each one has a leg of 3 and an hypotenuse of 5. Thus, each must be a 3-4-5 triangle. This allows us to see that the radius of the smaller circle is EC = 3 and the radius of the larger circle is BE = 4. From these, we could figure out the areas and then subtract these areas to find the area between them. This statement allows us to arrive at a numerical answer to the prompt question. Statement #1, alone and by itself, is sufficient.
Statement #2: This statement tells us something we already could figure out from the prompt information. Technically, this statement is tautological. A tautological statement is one that contains no new information, nothing new that we couldn’t figure out on our own; examples of tautologies are “My favorite flavor of ice cream is the flavor I like most” or “Today is the day after yesterday.” Like those statements, Statement #2 adds nothing to our understanding. Statement #2, alone and by itself, is not sufficient.
Answer = (A)
6) This is question that demands visual insight.
Statement #1: Think about these lengths. The top, KL is twice the length of the slanted sides, and the bottom, JM, is three times the length. This means that we could build this trapezoid from five equilateral triangles.
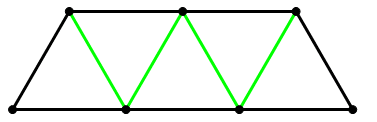
With other combinations of four lengths, we would be able to get different quadrilaterals resulting (e.g. changing the tilt of a rhombus). With these lengths (5, 10, 5, 15), there is no other quadrilateral possible. (Try this with physical items with lengths in the ratio 1:2:1:3 to see for yourself.) Thus, we know all the angles. We know that each equilateral has side of 5, so we could figure out the area of each equilateral, then multiply by five. Thus, we can find the area on the bases of this statement alone. Statement #1, alone and by itself, is sufficient.
Statement #2: If we know just this, then the shape could have any width. It could be relative narrow or a mile-wide. We cannot determine a unique area on the basis of this statement alone. Statement #2, alone and by itself, is not sufficient.
Answer = (A)
7) We know the area of the square, so the side of the square is
![]()
Thus, we know the length of the vertical leg, CE, in right triangle CEF, and we know the horizontal leg, BC, in right triangle ABC. Furthermore, these two triangles must be similar to teach other and similar to the larger triangle, ADF, because all the angles are the same.
Statement #1: We know triangle CDE is a half a square, so it’s a 45-45-90 triangle. Angle DCE = 45 degrees. Well,
(Angle ECF) = (Angle DCF) – (Angle DCE) = 75 – 45 = 30 degrees
This means that CEF is a 30-60-90 triangles, and so is triangle ABC because they are similar. In each, we know the length of one side, so we could find the other sides and solve for the areas. Thus, we could find the area of the entire triangle ADF. This statement leads directly to a numerical answer to the prompt question. Statement #1, alone and by itself, is sufficient.
Statement #2: This is interesting. We know that triangles ABC and CEF are similar, so they are proportional. Let AB:BC = r. Then CE:EF = r as well.

Now, notice that both BC and CE are sides of the square. Let BC = CE = s.
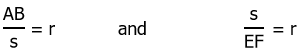
Now, multiply those two fractions together, and the s terms will cancel.
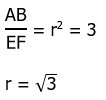
This the ratio of the longer leg to the shorter leg in the 30:60:90 triangle. We know the sides of the square, so we can find all the lengths in triangles ABC and CEF, which would allow us to find all the areas. Thus, we could find the area of the entire triangle ADF. This statement leads directly to a numerical answer to the prompt question. Statement #2, alone and by itself, is sufficient.
Each statement is sufficient on its own. Answer = (D)
8) We know the diameter of the circle is FJ = 40, so its radius is r = 20. FJ = 40 is also the base of the triangle in question. We need the height of the triangle in order to find its area.
Statement #1: We know point P is one of the two points where the circle intersects side GH, the top of the rectangle. We still don’t know how tall the rectangle is. We know the height must be less than 20, so that the circle can intersect it, but we certainly don’t know the exact height.
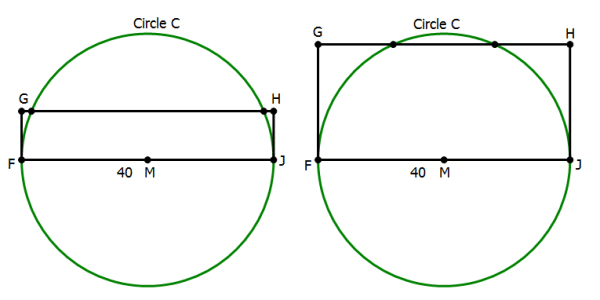
Without an exact height, we cannot compute an exact area. Statement #1, alone and by itself, is not sufficient.
Statement #2: Construct Point Q, the midpoint of GH, and draw in segments MQ and MR. MQ joins midpoints of opposite sides of a rectangle, so this would be perpendicular to both FJ and GH.
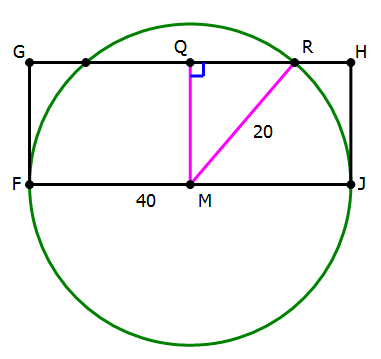
We know that MR is a radius, so it has a length of 20. We know that QH is half the length of GH, so QH = 20. We know that RH = 7. Notice
QR + RH = QH
QR = QH – RH = 20 – 7 = 13
Now, look at right triangle MQR. We know the hypotenuse MR = 20. We know the horizontal leg QR = 13. We could use that most extraordinary mathematical theorem, the Pythagorean Theorem, to find the length of QM. On GMAT Data Sufficiency, we don’t have to carry out the actual calculation: it results in an ugly radical expression anyway. It’s enough to know that we could find the numerical value of QM, the height of the rectangle.
We don’t know the exact position of point P, but it’s somewhere on GH, and every point on GH has the same height above FJ, so this height would be equal to the height of the triangle. Thus, we could find the height of the triangle, and therefore the area. On the basis of this statement, we could give a numerical response to the prompt question. Statement #2, alone and by itself, is sufficient.
Answer = (B)
9) Statement #1: This one guarantees that BD is a line of symmetry in the diagram, so triangle ABC would have to be isosceles, but it could be any one of a number of a different sizes & shapes.
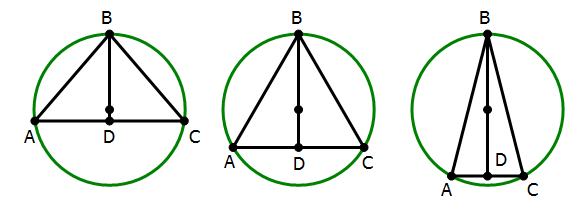
In all these examples, AB = BC and (angle A) = (angle C). The triangle could be equilateral, but it doesn’t have to be. These three examples have different areas, so this statement, by itself does not guarantee that we could calculate an exact area. Statement #1, alone and by itself, is not sufficient.
Now, forget all about statement #1.
Statement #2: We know that the radius is r = 6, so
![]()
Thus, we know that arc AB is 1/3 of the entire circumference. Therefore, it must occupy an angle of 1/3 of 360 degrees: arc AB must occupy 120 degrees.
In an equilateral triangle, all three angles would be 60 degrees and all three arcs would be 120 degrees. Here, all we know is that one arc, AB, is 120 degrees, and other two arcs could be other values. Thus, angle C must be 60 degrees, but other other angles can be other values.
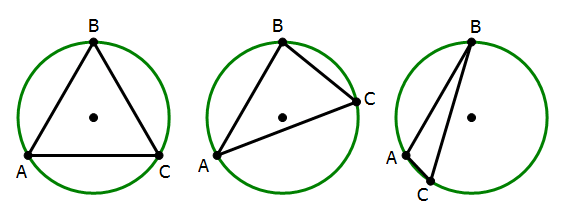
In all three of those diagrams, AB is a 120 degree arc and angle C is 60 degrees. The triangle could be equilateral, but it doesn’t have to be. Statement #2, alone and by itself, is not sufficient.
Now combine the statements. From the first statement, we know that AB = BC and (angle A) = (angle C). From the second statement, we know that (angle C) = 60 degrees. Well, that would mean that (angle A) = 60 degrees as well, and that leaves exactly 60 degrees for angle B. If we have three 60 degree angles, we know that ABC is equilateral. If we know the radius of a circle, then we can calculate the area of an equilateral triangle with its three vertices on the circle (this would involve subdividing the equilateral into six 30-60-90 triangles).
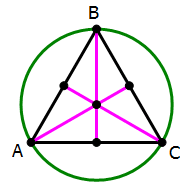
With the combined information of both statements, we can find a definitive answer for the prompt question. Together, the statements are sufficient.
Answer = (C)
10) Start with what we know from the prompt. We know BCGE is a rectangle with two parallel vertical sides that are perpendicular to two parallel horizontal sides.
We know that ABE and CGD are right triangles with the same length vertical legs and the same length hypotenuses, so by the Pythagorean theorem, the third sides must be equal, AE = DG, and the two triangles are equal in every respect.
We know that entirely figure is symmetrical around a vertical line down the middle. The trapezoid is entirely symmetrical, and isosceles triangle EFG is also symmetrical. Suppose we constructed the midpoint of EG and called it Q. Then, line MQ would be the symmetry line of both the trapezoid and the isosceles triangle. This line MQ would be parallel to BE and CG, and it would be perpendicular to BC and EG. If we extended MQ above and below the trapezoid, we would be guaranteed that point F would lie somewhere on this line.
For this problem, I am going to jump ahead to the combined statements. Statement #1 tells us that BCGE is a square. Statement #2 tells that the sides of the trapezoid are parallel to the sides of the isosceles triangle (by symmetry, the parallelism must be true on both the right and the left side). Even with all this information, we cannot give a definitive answer to the prompt question.
You see, the missing piece are the lengths of AE and DG. By the symmetry of the diagram, we know AE = DG, but we don’t know how this size compares to BM = MC. In the diagram, it appears that DG < MC, but because this is a GMAT DS diagram, we can’t believe sizes on the diagram.
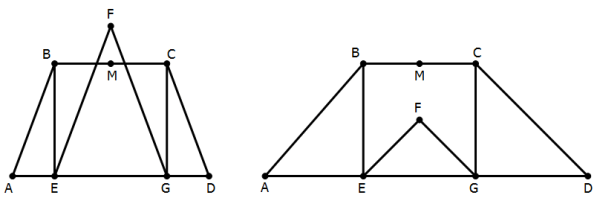
If DG < MC, then point F will be above M, outside of the trapezoid, as seen in the diagram on the left. If DG = MC, then point P will coincide with point M. If DG > MC, then point F will be below point M, inside the trapezoid.
Because we don’t know how the AE = DG length compares to the BM = MC length, we don’t know where point F falls, and we can’t give a definitive answer to the prompt question. Even combined, the statements are insufficient.
Answer = (E)






Leave a Reply