A lot of students prepping for GMAT Quant, especially those GMAT students away from math for a long time, get lost when trying to divide by a square root. However, dividing by square roots is not something that should intimidate you. With a short refresher course, you’ll be able to divide by square roots in no time.

Practice questions: How to divide by a square root
First, consider these three practice questions.
1. In the equation above, x =
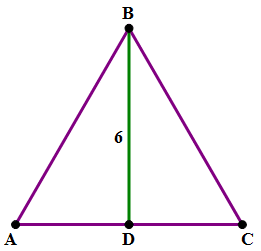
2. Triangle ABC is an equilateral triangle with an altitude of 6. What is its area?
3. In the equation above, x =
The second one throws in a little geometry. You may want to review the properties of the 30-60-90 Triangle and the Equilateral Triangle if those are unfamiliar. The first one is just straightforward arithmetic. The third is quite hard. For any of these, it may well be that, even if you did all your multiplication and division correctly, you wound up with an answers of the form —something divided by the square root of something—and you are left wondering: why doesn’t this answer even appear among the answer choices? If this has you befuddled, you have found exactly the right post.
Fractions and radicals
When we first met fractions, in our tender prepubescence, both the numerators and denominators were nice easy positive integers. As we now understand, any kind of real number, any number on the entire number line, can appear in the numerator or denominator of a fraction. Among other things, radicals—that is, square-root expressions—can appear in either the numerator or denominator. There’s no particular issue if we have the square-root in a numerator. For example,
is a perfectly good fraction. In fact, those of you who ever took trigonometry might even recognize this special fraction. Suppose, though, we have a square root in the denominator: what then? Let’s take the reciprocal of this fraction.
This is no longer a perfectly good fraction. Mathematically, this is a fraction “in poor taste”, because we are dividing by a square root. This fraction is crying out for some kind of simplification. How do we simplify this?
Dealing with square roots in the denominator
By standard mathematical convention, a convention the GMAT follows, we don’t leave square-roots in the denominator of a fraction. If a square-root appears in the denominator of a fraction, we follow a procedure called rationalizing the denominator.
We know that any square root times itself equals a positive integer. Thus, if we multiplied a denominator of the square root of 3 by itself, it would be 3, no longer a radical. The trouble is—we can’t go around multiplying the denominator of fractions by something, leaving the numerator alone, and expect the fraction to maintain its value. BUT, remember the time-honored fraction trick—we can always multiply a fraction by A/A, by something over itself, because the new fraction would equal 1, and multiplying by 1 does not change the value of anything.
Thus, to simplify a fraction with the square root of 3 in the denominator, we multiply by the square root of 3 over the square root of 3!
That last expression is numerically equal to the first expression, but unlike the first, it is now in mathematical “good taste”, because there’s no square root in the denominator. The denominator has been rationalized (that is to say, the fraction is now a rational number).
Sometimes, some canceling occurs between the number in the original numerator and the whole number that results from rationalizing the denominator. Consider the following example:
That pattern of canceling in the simplification process may give you some insight into practice problem #1 above.
Square roots and addition in the denominator
This is the next level of complexity when it comes to dividing by square roots. Suppose we are dividing a number by an expression that involves adding or subtracting a square root. For example, consider this fraction:
This is a fraction in need of rationalization. BUT, if we just multiply the denominator by itself, that WILL NOT eliminate the square root — rather, it will simply create a more complicated expression involving a square root. Instead, we use the difference of two squares formula, 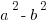 = (a + b)(a – b). Factors of the form (a + b) and (a – b) are called conjugates of one another. When we have (number + square root) in the denominator, we create the conjugate of the denominator by changing the addition sign to a subtraction sign, and then multiply both the numerator and the denominator by the conjugate of the denominator. In the example above, the denominator is three minus the square root of two. The conjugate of the denominator would be three plus the square root of two. In order to rationalize the denominator, we multiply both the numerator and denominator by this conjugate.
= (a + b)(a – b). Factors of the form (a + b) and (a – b) are called conjugates of one another. When we have (number + square root) in the denominator, we create the conjugate of the denominator by changing the addition sign to a subtraction sign, and then multiply both the numerator and the denominator by the conjugate of the denominator. In the example above, the denominator is three minus the square root of two. The conjugate of the denominator would be three plus the square root of two. In order to rationalize the denominator, we multiply both the numerator and denominator by this conjugate.
Notice that the multiplication in the denominator resulted in a “differences of two squares” simplification that cleared the square roots from the denominator. That final term is a fully rationalized and fully simplified version of the original.
Summary
Having read these posts about dividing by square roots, you may want to give the three practice questions at the top of this article another try, before reading the explanations below. If you have any questions on dividing by square roots or the explanations below, please ask them in the comments sections! And good luck conquering these during your GMAT!
Practice question explanations
1) To solve for x, we will begin by cross-multiplying. Notice that
because, in general, we can multiply and divide through radicals.
Cross-multiplying, we get
You may well have found this and wondered why it’s not listed as an answer. This is numerically equal to the correct answer, but of course, as this post explains, this form is not rationalized. We need to rationalize the denominator.
Answer = (D)
2) We know the height of ABC and we need to find the base. Well, altitude BD divides triangle ABC into two 30-60-90 triangles. From the proportions in a 30-60-90 triangle, we know:
Now, my predilection would be to rationalize the denominator right away.
Now, AB is simplified. We know AB = AC, because the ABC is equilateral, so we have our base.
Answer = (C)
3) We start by dividing by the expression in parentheses to isolate x.
Of course, this form does not appear among the answer choices. Again, we need to rationalize the denominator, and this case is a little trickier because we have addition in the denominator along with the square root. Here we need to find the conjugate of the denominator—changing the plus sign to a minus sign—and then multiply the numerator and denominator by this conjugate. This will result in:
Answer = (A)

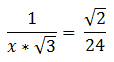
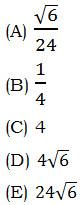
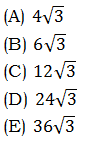
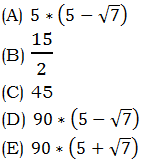
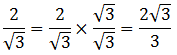
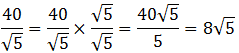
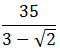
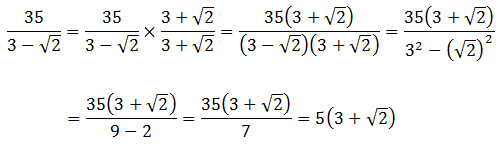
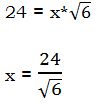
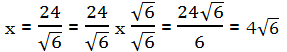
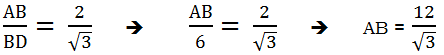
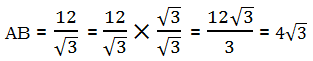
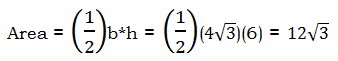
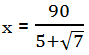
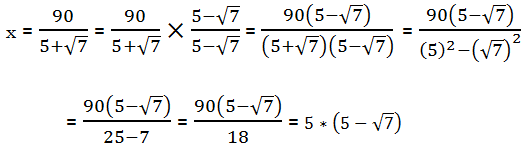





Leave a Reply