Here are eight practice problems on Sequences.
14, 23, 32, 41, 50, 59, …
1) In the sequence above, each term is 9 more than the previous term. What is the 40th term of the sequence?
- (A) 360
- (B) 365
- (C) 369
- (D) 374
- (E) 383
2) What is the difference between the fourth and third terms of the sequence defined by 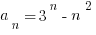
- (A) 18
- (B) 23
- (C) 47
- (D) 65
- (E) 83
3) Which of the following could be true of at least some of the terms of the sequence defined by
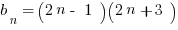
I. divisible by 15
II. divisible by 18
III. divisible by 27
- (A) I only
- (B) II only
- (C) I and II only
- (D) I and III only
- (E) I, II, III
4) Let S be the set of all positive integers that, when divided by 8, have a remainder of 5. What is the 76th number in this set?
- (A) 605
- (B) 608
- (C) 613
- (D) 616
- (E) 621
5) Let T be a sequence of the form 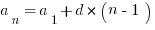 . If
. If 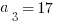 and
and 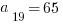 , find
, find 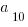 .
.
- (A) 37
- (B) 38
- (C) 39
- (D) 40
- (E) 41
6) What is the sum of all the multiples of 20 from 160 to 840?
- (A) 14,000
- (B) 17,500
- (C) 18,060
- (D) 28,000
- (E) 35,000
7) A sequence is defined by 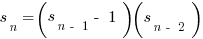 for n > 2, and it has the starting values of
for n > 2, and it has the starting values of 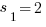 and
and 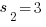 . Find the value of
. Find the value of 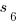 .
.
- (A) 25
- (B) 32
- (C) 36
- (D) 93
- (E) 279
9) In the set of positive integers from 1 to 500, what is the sum of all the odd multiples of 5?
- (A) 10,000
- (B) 12,500
- (C) 17,500
- (D) 22,500
- (E) 25,000
10) If 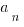 =
=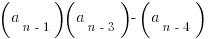 ,
, 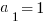 ,
, 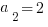 ,
, 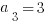 , and
, and 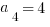 , what is the value of
, what is the value of 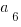 ?
?
- (A) 7
- (B) 11
- (C) 19
- (D) 42
- (E) 130
Solutions will follow this article.
Sequences
Sequences are a tricky topic on the GMAT Quant section. In that linked article, I discuss sequence notation, which is a variant of function notation, and I discuss recursive sequences, that is, sequences in which each term is determined by the previous term or terms.
Arithmetic Sequences
An arithmetic sequence is a sequence in which we add some fixed amount to each term to get the next term. Another way to say that is that, if we subtract any term from the following term, the difference will always be the same: this difference is called the common difference of the arithmetic sequence. Let d be the common difference. Then, in algebraic form, the terms of the arithmetic sequence would be
Recall that, say, for the 3rd term, the little subscript 3 is the index, that is, the position on the list. For this particular sequence, every term equals the first term plus a factor times d, and that factor is always one less than the index. This means we can write the general term as:
That is a very important formula, although, as always, don’t just memorize it; instead, remember the logic of the argument that leads up to it.
This is an important formula because any evenly spaced list is an arithmetic sequence. The consecutive multiples of any factor form an arithmetic sequence.
The sum of the first n terms in an arithmetic sequence is given by the formula
That’s the sum of the first term and the last term, times half the number of items on the list. You can also thing of that as the average of the first & last terms times the number of items on the list. One special case is the sum of the first n integer, given by
Summary
If you had some insights while reading that first article on sequences or the section on arithmetic sequences, then take another look at the problems above before looking at the solutions below. If you found this article helpful, or if you have an alternative solution for solving any of these problems, please let us know in the comments section below!
Practice problem explanations
1) This is an arithmetic sequence, with
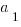 = 14 and d = 9
= 14 and d = 9
Using the formula for the nth term, we find that:
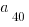 = 14 + 9*39 = 14 + 351 = 365.
= 14 + 9*39 = 14 + 351 = 365.
Answer = (B).
2) This is general sequence, with an explicitly defined nth term.
Answer = (C).
3) First of all, if n = 8, then
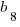 = (16 – 1)(16 + 3) = 15*19
= (16 – 1)(16 + 3) = 15*19
We don’t have to calculate that: clearly, whatever it is, it is divisible by 15. Similarly, if n = 12, then
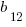 = (24 – 1)(24 + 3) = 23*27
= (24 – 1)(24 + 3) = 23*27
Whatever that equals, it must be divisible by 27. Thus, I & III are true. Notice that, for any integer, 2n must be even, so both (2n – 1) and (2n + 3) are odd numbers, and their product must be odd. Every term in this sequence is an odd number. Now, no odd number can be divisible by an even number, because there is no factor of 2 in the odd number. Therefore, no terms could possibly be divisible by 18. Statement II is absolutely not true.
Answer = (D).
4) Think about the first few numbers on this list:
5, 13, 21, 29, 37, 45, …
Notice that 5 is the first number in S, because when 5 is divided by 8, the quotient is zero and the remainder is 5.
This is an arithmetic sequence with
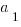 = 5 and d = 8
= 5 and d = 8
Using the general formula for the nth term of an arithmetic sequence, we have
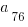 = 5 + 8*(75) = 5 + 4*(150) = 5 + 600 = 605
= 5 + 8*(75) = 5 + 4*(150) = 5 + 600 = 605
Answer = (A).
5) The formula in the first sentence tells us that this is an arithmetic sequence. The first term and the common difference are unknown, but we can generate two equations from the values of the two terms given.
Subtract the first equation from the second, and we get 16d = 48, which means d = 3. From the value of third term, we can see that first term must equal 11. Therefore,
Answer = (B).
6) This is arithmetic sequence, and we have the first and last terms already. How many terms are there? Well, 160 = 20*(8) and 840 = 20*(42); we have to use inclusive counting to see that there are 42 – 8 + 1 = 35 terms.
Answer = (B).
7) This is a recursive sequence, and we have to find it term by term.
Answer = (E).
8) This is a recursive sequence, so we have to work backwards term by term.
Answer = (A).
9) Let’s think about the terms in this sequence:
5, 15, 25, 35, …., 485, 495
The first term is 5 and the last is 495. There are 100 multiples of 5 from 1 to 500, so there are 50 odd multiples and 50 even multiple. The sum is:
Answer = (B).
10) This recursive sequence is probably more difficult than anything that the GMAT is going to throw you, but solving this problem is not too bad. As with any recursive sequence, we have to go term by term.
Answer = (C).


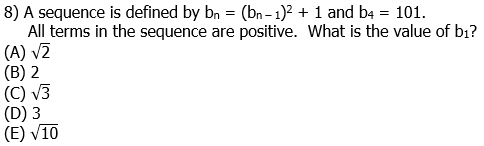
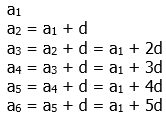
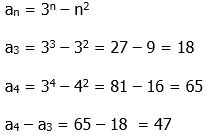
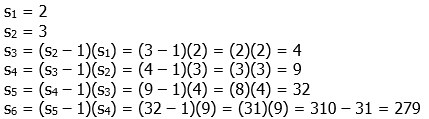
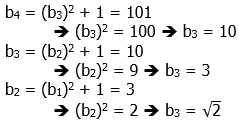
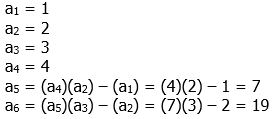



Leave a Reply