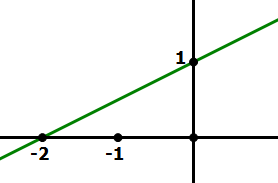
1) The line shown passes through the point (A, 30). Which of the following is closest to the value of A?
-
(A) 58
(B) 59
(C) 60
(D) 61
(E) 62
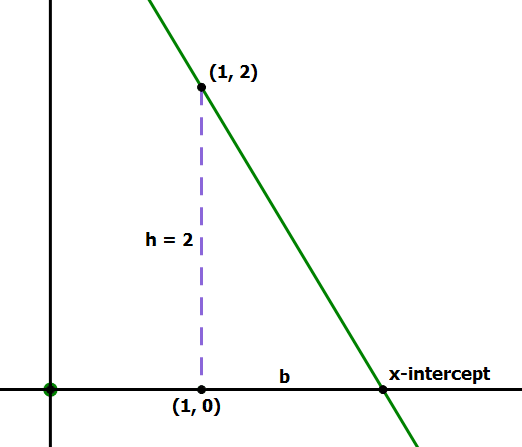
2) Line A has a slope of 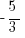 and passes through the point (–2, 7). What is the x-intercept of Line A?
and passes through the point (–2, 7). What is the x-intercept of Line A?
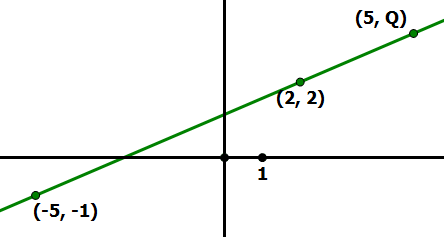
3) Line J passes through the points (– 5, – 1), (2, 2), and (5, Q). What is the value of Q?
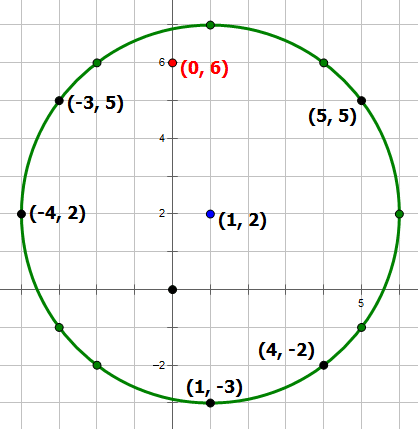
4) A circle has a center of (1, 2) and passes through (1, –3). The circle passes through all of the following EXCEPT:
-
(A) (–4, 2)
(B) (–3, 5)
(C) (0, 6)
(D) (4, –2)
(E) (5, 5)
5) Points J (3, 1) and K (– 1, – 3) are two vertices of an isosceles triangle. If L is the third vertex and has a y-coordinate of 6, what is the x-coordinate of L?
-
(A) –3
(B) –4
(C) –5
(D) –6
(E) –7
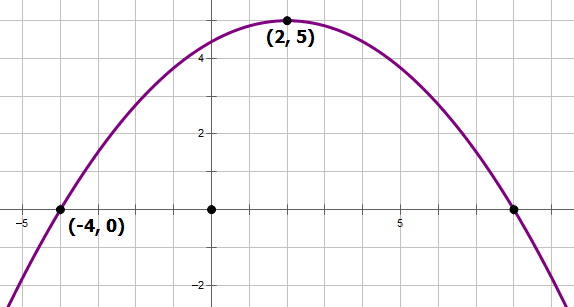
6) A parabola has one x-intercept at (– 4, 0). If the vertex is at (2, 5), find the other x-intercept.
-
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
Coordinate Geometry
The coordinate plane is also known as the x-y plane and the Cartesian plane, so named after its discoverer, Mr. Rene Descartes (1596 – 1650), the mathematician & philosopher who also said “I think therefore I am.” Of course, it consists of two perpendicular numbers lines, the x- and y-axis, which define a grid that covers the entire infinite plane. Here are some previous blogs on this most remarkable mathematical object, the coordinate plane:
2) Lines & Slopes in the x-y plane
3) Midpoints and Parallel & Perpendicular Lines
5) Special Properties of the line y = x
6) an earlier set of Coordinate Geometry practice questions
7) a set of challenging Coordinate Geometry practice questions
If you get some insights from some of those blogs, you might give the problems above a second look before reading the solutions below.
Practice problem explanations
1) The line appears to have a slope of ½ and y-intercept of 1, so its equation would be
y = 0.5x + 1
Plug in A for x and 30 for y.
30 = 0.5A + 1
29 = 0.5A
58 = A
Answer = (A)
2) Think about this visually. A slope of – 5/3 means, among other things, left 3 spaces, down 5. If the line goes through the point (–2, 7), then it must also go through (1, 2), which is must closer to the x-intercept. Let’s think about this in the vicinity of the x-intercept.
Obviously, (1, 2) is at a height of 2 above the x-axis. Let b be the distance from (1, 0) to the x-intercept. We know –h/b must equal the slope.
Now, we just have to add one to that to get the horizontal distance from the origin.
Answer = (B)
3) Think about this visually. From (–5, –1) to (2, 2), the line moves right 7 and up 3, so that’s a slope of 3/7.
From the point (2, 2) to the point (5, Q), there’s a horizontal distance of 3, an unknown vertical distance — call it h, so that h = Q – 2, or Q = h + 2. The ratio of this vertical and horizontal distance must equal the slope.
That’s h. Now, add 2 to get Q.
Answer = (C)
4) The radius is r = 5. First of all, 5 above the center, the circle goes through (1, 7) on the top, and 5 to the left & right of the center, the circle goes through (–4, 2) and (6, 2) on the same horizontal line as the center. That first point is choice (A).
That length of 5 can also be the hypotenuse of a 3-4-5 slope triangle, so starting from the center (1, 2), we could go over ±3 and up ±4, or over ±4 and up ±5. This means the circle must go through
right 3, up 4 = (4, 6)
right 4, up 3 = (5, 5) = option (E)
right 3, down 4 = (4, –2) = option (D)
right 4, down 3 = (5, –1)
left 3, up 4 = (–2, 6)
left 4, up 3 = (–3, 5) = option (D)
left 3, down 4 = (–2, –2)
left 4, down 3 = (–3, –1)
That’s all the points other than option (C). Notice that (–2, 6) and (4, 6) are on the circle, so another point between them, on the same horizontal line, (0, 6), could not be on the circle.
Answer = (C)
5) This one looks like it could involve a very complicated calculation, but there’s a very elegant way to do it. This involves special properties of the line y = – x. Notice that the coordinates of J & K have been switched, x for y and vice versa, and they have the opposite ± signs. This means that J and K are reflections of each other over the mirror line y = – x. As is always true of any reflection, every point on the mirror line is equidistant from a point and its reflection. Thus, we just need any point on the line y = – x, for example, (–6, 6).
Answer = (D)
6) The line of symmetry of a parabola always passes through the vertex, so the equation of the line of symmetry is the vertical line x = 2. The two x-intercepts are symmetrical around this line. The point (– 4, 0) is six units to the left of the symmetry line, so the other should be six units to right, at (8, 0).


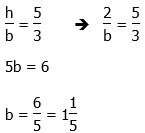



Leave a Reply