SAT math includes the whimsically-named (and slightly intimidating) section “Passport to Advanced Math.” The good news is that it is actually not advanced math. It’s actually the skills that underpin some of the more advanced stuff you’ll be doing in calculus and pre-calculus. In this light, the name passport doesn’t seem as fanciful, since in order to travel in the land of advanced math you’ll need a “passport” showing that you have the fundamentals down.
Passport to Advanced Math includes 16 of the 58 questions spread out over the two math sections. If you’re already comfortable with the other math and are shooting for that perfect Math score, you should definitely spend more time in this area. In this post, we’ll look at some critical concepts under the SAT Passport to Advanced Math category, along with some practice questions!
Table of Contents
- Exponents and Roots in SAT Passport to Advanced Math Questions
- Quadratic Equations
- Bigger Polynomials
- Coordinate Geometry
- Additional Topics in SAT Passport to Advanced Math
Exponents in SAT Passport to Advanced Math Questions
You are likely to see a few exponents on the SAT. Exponents often times scare the bejeezus out of students. The word exponent alone conjures up numbers so big that they seemingly dwarf the number of atoms in the known universe. But do not fear: there are no atoms on the test, and the exponents on the SAT deal with far smaller numbers. In order to have a chance on the harder questions, you’ll have to first know your basics.
Once you are consistently doing well on these, you won’t have to worry about exponents. The thing, though, is it is very easy—especially during the stress of the actual exam—to make simple (and easily avoidable!) mistakes regarding exponents.
First, watch one of Magoosh’s SAT experts, Chris, discuss exponents in SAT Passport to Math questions; then, we’ll dive into the topic in slightly more depth!
SAT Exponent Basics: What You Need to Know
#1: The base (it’s the big number)
An exponent all alone would be nothing more than a tiny speck floating in space. Every exponent needs a base:
\(3^2 \): base 3
\(2^5\) : base 2
#2: Don’t add or subtract the bases
\(3^2+2^2\) does NOT equal \(5^2\)
\(6^2-3^2\) does NOT equal \(3^2\)
#3: When multiplying the same bases, add the exponents; when dividing, subtract
\(3^2(3^5) = 3^7\)
\(2^4(2^4) = 2^8\)
\(3^{10}/(3^5) = 3^5\)
\(2^4/(2^2) = 2^2\)
It’s also important to see how this plays out with variables:
\({x^y}*{x^z}=x^{y+z}\)
\({x^y}/{x^z}=x^{y-z}\)
It’s pretty easy to see why rule #3 exists if we use actual numbers and expand the equation:
\( {2^2}*{2^3}=2^{2+3}=2^5\)
\({2^2}=2*2\)
\({2^3}=2*2*2\)
\({2^2}*{2^3}=2*2*2*2*2=2^5\)
Be careful that you only do this when the bases are the same!
\(3^2(2^5) ne 6^7\)
#4: When taking both a base and exponent to an exponent, multiply the exponents; when taking the root, divide
When you have a power of a power, you can multiply those exponents. Don’t add them!
\((4^2)^3\) does NOT equal \(4^5\) or \(4^8\)
\((4^2)^3 = 4^6\)
Since roots are the opposite operation of powers, just like division is the opposite of multiplication, you can divide an exponent by the radical.
Again, if we use real numbers and expand it, the reasons why are pretty clear.
\((2^3)^2=2^(3*2)=2^6\)
\((2^3)^2=(2*2*2)^2=(2*2*2)*(2*2*2)=2^6\)
\(sqrt[3]{2^6}=2^{6/3}=2^2\)
\(sqrt[3]{(2*2)*(2*2)*(2*2)}=(2*2)=2^2\)
When using variables, this is what this rule looks like:
\((x^y)^z=x^{y*z}\)
\(sqrt[z]{x^y}=x^{y/z}\)
#5: Sometimes you’ll need to distribute exponents and roots
\((xy)^z={x^z}{y^z}\)
\(sqrt[z]{xy}=sqrt[z]{x}sqrt[z]{y}\)
If you have an exponent outside of parentheses that contain two multiplied numbers, you need to find the power of both factors.
\((2*3)^2=6^2=36\)
\( (2*3)^2={2^2}*{3^2}=4*9=36\)
\((2*3)^2 ne 2*{3^2}\)
And there’s another common exponent mistake made in this kind of situation: don’t distribute exponents to terms inside the parentheses that are added or subtracted.
\((x+y)^z ne {x^z}+{y^z}\)
The FOIL method makes it pretty clear why that doesn’t work.
Radicals follow the same rules. If you have numbers under the radical that are added, then you can’t just find the root of each one. You have to combine them first.
But you can take a number under a radical, break it into factors, and simplify it that way.
\(sqrt[3]{56}=sqrt[3]{8*7}=sqrt[3]{8}sqrt[3]{7}=2sqrt[3]{7}\)
Knowing this comes in handy on the SAT.
#6: The SAT may throw radicals other than square roots at you
Numbers over radicals occasionally throw people off. Just remember that it’s the opposite process of exponents. So if \(2^3\) is \(2*2*2=8\), then \(sqrt[3]{8}=2\). This is totally fundamental, but it’s a good place to start.
#7: The SAT may throw fractions in exponents at you
These are just the same as above. If you see a fraction in an exponent on your SAT, go right ahead and convert it into a radical if that helps. So \(8^{1/3}\) equals 2, just the same as \(sqrt[3]{8}=2\).
If you have something other than a 1 in the numerator, like \(8^{2/3}\), then just put the denominator into the radical and keep the numerator as an exponent: \(sqrt[3]{8^2}\). From there, it doesn’t matter which operation you carry out first. \(2^2=4\) just as \(sqrt[3]{64}=4\).
#8: The SAT may throw a zero exponent at you
Any number to the 0th power is one. \(2^0=1\) and \(9,999^0=1\). We don’t need to worry about why for the purposes of the SAT (but if you enjoy math puzzles and want to figure it out, here’s a hint: it has to do with the next rule).
#9: The SAT may throw a negative exponent at you
Careful not to get \(x^{-2}\) confused with \(x^{1/2}\). Instead, \(x^{-2}=1/x^2\). Although fractions in exponents are tested more often, negatives are also liable to show up on your SAT, so you should get comfortable with this if you aren’t already.
How you can imagine this concept using gummy bears or whatever, I’m not sure, but that doesn’t make it difficult to use—and that’s true for all of the rules above. As long as you know the facts, you can work pretty easily with exponents on your SAT that might seem daunting at first.
Now that we’ve gone through everything you’d need to know about exponents and roots, let’s try our hand at a practice problem:
Practice with Exponents
A. \(16^{frac{1}{8}}\)
B. \(4^{frac{7}{16}}\)
C. \(4^{frac{1}{8}}\)
D. \(4^{frac{5}{8}}\)
Click here for the answer and explanation
Answer: C. \(4^{frac{1}{8}}\)
Wondering why C. is the answer? Click here for a video explanation!
Quadratic Equations in SAT Passport to Advanced Math
The SAT wants you to be able to deal not just with linear equations, as you do in the Heart of Algebra section, but polynomials. And the most common polynomial you’ll have to deal with are quadratic equations.
What Do Quadratic Equations Look Like?
The basic form of a quadratic function is this: \(f(x)=a{x}^2+bx+c\)
(Also note that this is the same as \(y=ax^2+bx+c\).)
Any time you see an equation that looks like that, you can graph it as a parabola.
\(y=5x^2+2x+3\) would be quadratic, for example. \(a=5\), \(b=2\), and \(c=3\).
In your introductory algebra classes, you were probably taught the reverse FOIL method to solve quadratics. The second-degree polynomials (i.e., quadratics) you end up seeing on Passport to Advanced Math can, unsurprisingly, be solved using reverse FOIL.
Take \(x^2-4x-5 = 0\) as an example.
To use reverse FOIL for a given quadratic, here are the steps:
- Find two numbers in which the product equals \(c\) (\(-5\) in the equation) and the sum equals \(b\) (\(-4\) in the equation). In this case, if you multiply \(-5\) and 1, you’ll get \(-5\), and if you add \(-5\) and 1, you’ll get \(-4\).
- Using these numbers, you can now solve the equation: \((x-5)(x+1) = 0\)
Quadratic Equation Patterns
Being familiar with FOIL and reverse FOIL is foundational to success on Passport to Advanced Math, but there are two patterns that can help you bypass FOIL/reverse FOIL entirely: perfect squares and difference of squares.
Perfect squares refers to the following expression: \((x+b)^2 = x^2 + 2bx + b^2\).
When you’re familiar with this expression, you would be able to FOIL an expression like \((x+2)^2\) and reverse FOIL an expression like \(x^2 + 10x + 25\) in no time.
Click here for the answer and explanation
Answer: \(x^2 + 10x + 25 = (x+b)^2 = (x+5)^2\)
By comparing the expression \((x+2)^2\) to \((x+b)^2\), we can replace 2 with \(b\) and see that \((x+2)^2 = (x+b)^2 = x^2 + 2bx + b^2 = x^2 + 2(2)(x) + 2^2\), which equals \((x+2)^2 = x^2 + 4x + 4\).
Now, let’s compare \(x^2 + 10x + 25\) with \(x^2 + 2bx + b^2\). The quickest way to solve this is to note that \(25 = 5^2\), which means that \(b\) has to equal 5. Replacing the \(b\) in \(2bx\) with 5, you can see that \(2(5)x = 10x\), which is what we have in the expression. So the simplified version is \(x^2 + 10x + 25 = (x+b)^2 = (x+5)^2\)
Difference of squares refers to the following expression: \((x+b)(x-b) = x^2 – b^2\). You’re probably wondering what happened to the middle coefficient. When you actually use FOIL on an expression like \((x+b)(x-b)\), you’ll see that the middle coefficient cancels out: \(x^2\) \(- bx + bx \) \(+ b^2\).
Let’s see how this pattern works when you replace \(b\) with 4: \((x+4)(x-4) = x^2 – b^2 = x^2 – 4^2 =\) \(x^2 – 16\)
If you’re not already comfortable with perfect squares and difference of squares, I highly recommend trying out different expressions where \(b\) = 1, 2, 3, etc. For example, using these formulas, try to figure out what’s \((x+1)^2\), \((x+1)(x-1)\), \((x+2)^2\), \((x+2)(x-2)\), and so on. These expressions come up a lot on the SAT, so recognizing them off the bat will really help you save time.
Quadratic Formula
Sometimes, reverse FOIL is not enough to solve quadratics. In that case, you’ll need the quadratic formula or
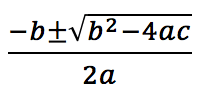
Before you freak out—the quadratic formula has that effect on students—let’s apply it to a real quadratic equation:
In this case, there are no integers whose product is \(-5\) and that sum to \(-5\). For instance, the only factors of \(-5\) are 1/\(-1\) and 5/\(-5\). None of those will sum to \(-5\). So in order to find out which two numbers, when multiplied equal \(-5\), but when added equal \(-5\), we have to use the quadratic formula.
Comparing \(x^2-5x-5 = 0\) to the expression \(ax^2-bx-c = 0\), you can see that a = 1, b = -5, and c = -5.
Plugging those values into the quadratic formula we get:
\(frac {5 pm sqrt{25+20}}{2}\)
\(frac {5 pm sqrt 5}{2}\)
When should I expect the quadratic formula on the SAT?
Click here to learn more
If the quadratic formula is not your friend, then you’re largely in luck. Based on the official tests we have at our disposal, it seems that there aren’t too many questions that require the use of the quadratic formula. But you want to be prepared for them if you encounter them.
So when do you know to use the quadratic formula?
- One indication is when the product of two integers can not result in \(b\).
- Another giveaway is when the answer choices have a radical sign and a plus or minus sign. Something like this: \(4 pm sqrt {2}\)
Even though the quadratic formula may not come up for you, being aware of these patterns and memorizing the quadratic formula could go a long day on test day. If you happen to face one or two questions that can only be solved using the quadratic formula, not even having a chance at these questions can hurt you psychologically because these would be such easy points to score if you had just remembered the formula.
So, while two points might seem minuscule, that psychological effect can reverberate throughout the rest of the math section!
Okay, my intention here is not to scare you. It is to give you the necessary tools. In this case, simply memorize the quadratic formula, do a few practice questions using this concept, and on test day you won’t be bullied by this concept.
Practice with Quadratic Equations
What is the solution set for the above equation?
A. \(-2\)
B. \(-2, -5\)
C. \(-5\)
D. No solutions.
Click here for the answer and explanation
Answer: A. \(-2\)
This may not look like a quadratic equation question. But in order to solve for ‘x’ we want to remove the square root sign. To do so, we have to square both sides, giving us:
Balancing the equation gives us:
\((x+5)(x+2)\)
\(x = -5\) and \(-2\)
This seems like a pretty straightforward question, but here’s the twist: whenever you have a square root sign over the variable one side of the equation, watch out for the quantity under the variable equaling a negative when you plug the value back in. The reason is if you get a negative number underneath the square root sign, you do not have a valid solution.
Another possibility in which one of the ‘x’s you solve for is not valid, is if one side of the equation is a square root sign and the other side of the equation (the one that does not have a square root sign) is a negative number. The reason is that the radical sign (more commonly known as the square root sign) actually means the POSITIVE square root of a given number. So, when we see a radical sign in a question, the question is asking about the positive square root.
This is what is going on here, since when you plug in \(x = -5\) into the original equation you end up getting the following:
This is not valid, so therefore \(-5\) is not an answer. Only \(-2\) is, giving us A.
Bigger Polynomials
On the SAT, sometimes you have to deal with polynomials in which the powers can be very high, as in the following:
The key to dealing with polynomials of powers higher than three on the SAT is usually simplifying them. This is typically a matter of factoring an \(x\) or an \(x^2\) out of each term until you’re left with a simple quadratic in the parentheses. However, if you’re presented with something more complicated, you may want to use the answer choices as clues for how to break the quadratic down.
Practice with Polynomials
A. \(a^4 (9a^4-4a)\)
B. \((3a^4-2a^4)(3a^4+2a^4) \)
C. \((3a^4-2a^2)(3a^4+2a^2) \)
D. \(a^4 (3a-2)(3a+2) \)
Click here for the answer and explanation
Answer: D. \(a^4 (3a-2)(3a+2) \)
Remember, when you encounter polynomials, try to simplify it. You can see that you can factor out an \(a^4\) to give \(a^4(9a^4 – 4)\).
At this point, you only have two choices, A. and D. Be careful to not get tricked by A., which added an extra ‘a’ to the 4.
And if you’re comfortable with the difference of squares pattern (\((x – b)(x + b), or x^2 – b^2\)), you would be able to quickly confirm that \((3a-2)(3a+2)\) does equal \(9a^4 – 4\).
Coordinate Geometry
Other topics include the graphs of complex polynomials. The point of the test, though, isn’t to throw ridiculously complex equations at you; it wants to test your ability to recognize simple patterns in all that complexity. In other words, can you navigate around all the noise to find a relatively straightforward approach to solving the question?
When testing your knowledge about quadratics, functions, and polynomials, College Board is essentially interested in your ability to understand “relationships between algebraic and graphical representations of functions.” However, we’re going to use some less grand, simpler terms.
Coordinate geometry, or more colloquially, graphing, is another area which is filed under SAT Passport to Advanced Math, as long as (and here’s the important part) the equation is a polynomial. Most of the time, this will mean a parabola. Sometimes, though, you’ll get a graph of some monstrous polynomial like \(y^5+3y^4-2y^2+1\).
The good news is you’ll probably only have to decipher the graph to figure out how many times it crosses through the x-axis or something else relatively straightforward.
It’s really the parabola that is going to show up more often. What you need to know is that parabolas are symmetrical, meaning that each side occupies the same area on both sides of either y-axis or x-axis.
The equation of a parabola can be defined as \(f(x)= ax^2+bx+c\), where \(a\), \(b\), and \(c\) are constants (meaning they are some fixed number). Since \(a\) will often equal 1, it helps knowing good-old-fashioned FOIL, as you’ll see in the first practice question below.
Quadratic Graphing Shortcuts
Since the SAT doesn’t ask you to actually draw any graphs, we won’t focus on that. You may be able to find the answer to the question without even needing to know how to do this. Instead, let’s look at a few shortcuts.
Shortcut #1: a shows the direction of the parabola
Click here to learn more about this shortcut
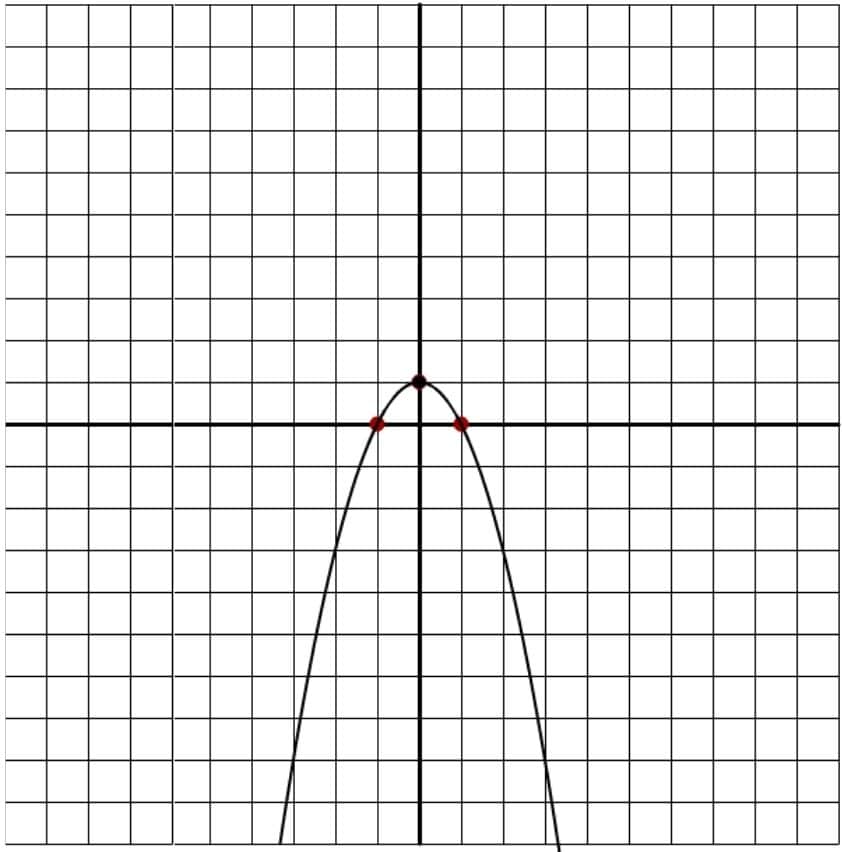
The value of \(a\) will show you whether the parabola it represents is positive or negative. So if \(a\) (the number multiplying \(x^2\)) is negative, the curve will open downward.
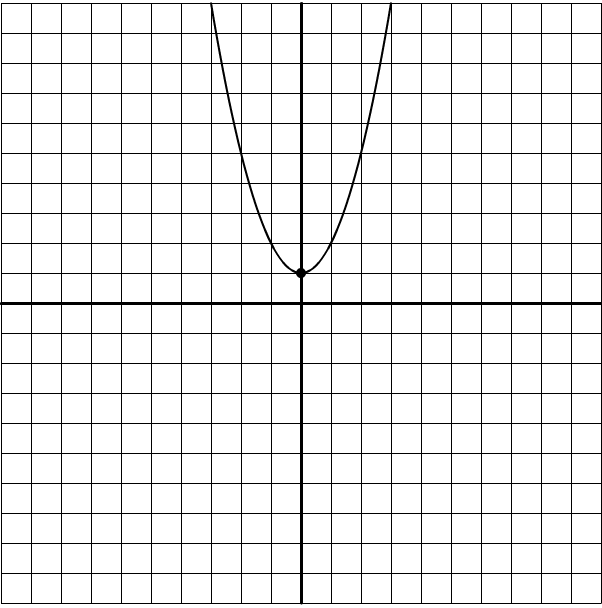
And the other way around is also true; if \(a\) is positive, the curve will open upward.
Shortcut #2: c shows the y-intercept
Click here to learn more about this shortcut
Let’s look at that quadratic function form again.
If \(x=0\), then \((fx)=c\), since we can take out both of those \(x\) terms. That’s the y-intercept, where the function crosses the y-axis. In the two graphs above, the y-intercept is the same: 1. That means any equation for either of those graphs would have to include a +1 at the end of it.
On the other hand, if the graph looked like this…
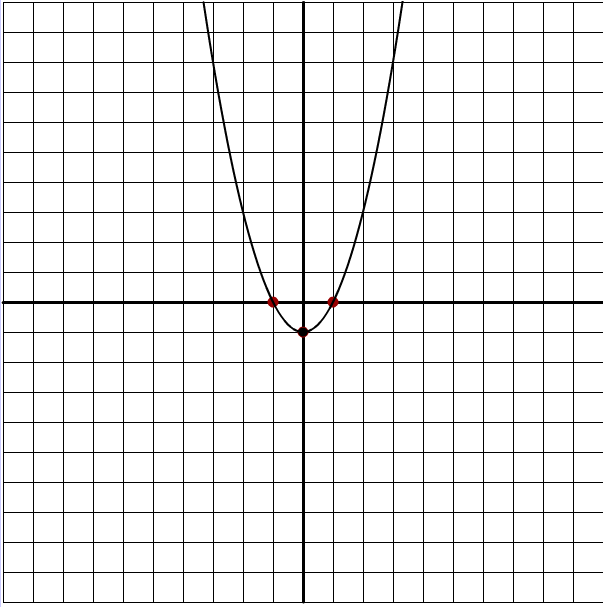
…then \(c\) would have to be \(-1\). That’s where the curve crosses the y-axis.
Shortcut #3: Use reverse FOIL to find the x-intercepts
Click here to learn more about this shortcut
Let’s say you’re asked to find the x-intercepts (the value of \(x\) when \(y = 0\)) of \(y = x^2-4x-5\).
If you’re comfortable with reverse FOIL to convert this equation to its root form, we can easily and quickly answer that question.
If you remember this equation above when we first discussed reverse FOIL, we know that the root form of this equation is \(y = (x-5)(x+1)\). Once you’re comfortable with identifying roots in the root form, you can see that the x-intercepts—also known as roots—are 5 and \(-1\). (We get this by setting the equation equal to 0 in order to find the values of \(x\) when \(y = 0\): \(0 = (x-5)(x+1)\)).
Shortcut #4: Know the parabola formula to find the vertex
Click here to learn more about this shortcut
Sometimes, the test might ask you to find something that requires a little more knowledge of parabolas. One useful form is \(y=a(x-h)^2+k\), where \(a\), \(h\), and \(k\) are constants and \((h,k)\) is the vertex of the parabola.
Let’s take the following equation as an example:
You can convert this quadratic to its root form by “completing the square,” which goes a bit something like this:
- Focus on the \(b\) in the equation, which is \(-6\), and divide by 2, which is \(-3\).
- Square \(-3\) to “complete the square,” which is 9.
- The equation then becomes \(y =\) \(x^2 – 6x + 9\) \(+ 5\).
- Using the concept of perfect squares, we can simplify the green part of the equation to its root form, which will lead to \(y =\) \((x – 3)^2\) \(+ 5\).
- We can see that \(h = 3\) and \(k = 5\), so the coordinates of the vertex is \((3, 5)\).
Shortcut #5: Use a graphing calculator, but only if you need to!
Click here to learn more about this shortcut
Based on the above shortcuts, you can usually eliminate a couple of equations or graphs from the answer choices pretty quickly. Then, just put in whatever info you can into your calculator.
If the question is asking about some general trend and doesn’t include specific values for \(a\), \(b\), and/or \(c\), then check if you can plug some in to see the pattern.
If you don’t have a graphing calculator, then just take it one point at a time. If \(x\) is 1, what is \(y\)? If \(x\) is 2? And so on.
Practice with Coordinate Geometry
Practice Question 1
Click here for the answer and explanation
Answer: 6
Really, all we are doing here is old-fashioned FOIL so that can find out the solutions for \(x\). Those solutions are the same as an x-intercept, since when you plug either value for x back into the equation, \(f(x)\), or the y-coordinate, will equal 0.
\((x-4)(x-2)\)
\(x=4\) and \(x=2\)
The sum equals 6.
Practice Question 2
A. \(f(x)=(x-1)^2-25\)
B. \(f(x)=(x-6)(x+2) \)
C. \(f(x)=(x+6)(x-2) \)
D. \(f(x)= x(x-2)-24 \)
Click here for the answer and explanation
Answer: A. \(f(x)=(x-1)^2-25\)
The great thing about this question is that knowledge about the vertex form, \(a(x-h)^2+k\), is enough to solve this question; you don’t actually have to plug anything in.
Using this equation, we can automatically get rid of choices B. and C. because they are in factored form, not vertex form. D. is not in vertex form either, so the only option is A.
If you come across questions like this on the SAT, you’re usually able to solve it faster by using the answer choices and process of elimination (also known as backsolving) than by actually using the formulas. But I’ll also show you how A. is the right answer by completing the square in order to get to the vertex form:
Using the four-step process from Shortcut #3, we can see that \(x^2-2x-24\) is the same as \(x^2-2x+1-24-1 \).
Notice how the two ‘1’s cancel each other, thereby leaving us with the original equation. Why did we even put the ‘1s’ in the first place? Well, \(x^2-2x + 1\) becomes \((x-1)^2\) when we complete the square.
So now I have: \((x-1)^2-25. \)
Therefore, \(h\) is equal to 1 and \(k\) is equal to \(-25\). So the vertex is \((1, -25)\). But the question did not ask us to write the vertex out; rather, it asked for the way we could best identify it. That’s the equation directly above, which is A.
Additional Topics in SAT Passport to Advanced Math
The one thing to know about SAT Passport to Advanced Math is that it loves to combine topics. As such, these question types could easily get you flustered on test day. Knowing what to expect is half the battle.
This post covers the most common content for this question type, but you may also see:
- Complex numbers
- Trigonometry
- Systems of Equations
- Function Notation
- Interpreting and Analyzing More Complex Equations in Context
To get a sense of all the different types of concepts that pop up in the SAT Passport to Advanced Math section, check out the Official Study Guide. Take the practice tests to see the 16 questions per test. If you miss a question because of conceptual misunderstanding, you’ll want to go back and review the content in this section of the Study Guide—or bookmark this page to come back to!






Leave a Reply