Integration, along with differentiation, is one of the two main operations in calculus. Where differentiation is a tool that allows us to examine rates of change, the integral is a tool that allows us to add up infinitesimal pieces of a whole.
More on integration
It is best to explore integration with an example. Imagine we had an irregular shape that we wanted to find the area of. If we divided the shape into regular rectangles, we could add up the area of all the rectangles and find the approximate area of the entire shape.
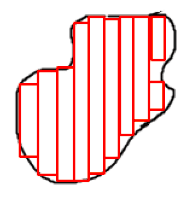
If we now took those rectangles and made them thinner and thinner, our approximation of the area of the whole would become more and more accurate. Eventually, as the rectangles became infinitely small (and with that, an infinite number of them), we would perfectly be able to find the area of the original shape. This is what the tool of integration allows us to do. It is therefore used to find concepts such as displacement, area, and volume.
Integration is very closely related to differentiation through The Fundamental Theorem of Calculus. (This will be discussed in its own article soon). In its simplest form, the operation of integration is the opposite of differentiation. It is therefore first introduced in calculus classes in the form of an antiderivative.
What is an antiderivative?
The antiderivative of a function is a new function whose derivative brings us back to the original function. For example, if we have a function f(x) = 3x2, the antiderivative would be F(x) = x3 + c (where c is a constant), because the derivative of F(x) brings up back to our original function. This is also known as an indefinite integral.
The notation for indefinite integrals is the following:
![]()
For example:
![]()
We should notice that there is a little “dx” at the end of our integration. This means that we are taking our integral ‘with respect to x’. This is the same dx that we see at the top of our differentiation notation. When we study multi-variable calculus, this will become very important.
We should also notice a c at the end of F(x). This represents a constant. We have to put this here because we do not, without outside information, know what this constant could be. When we take the derivative of F(x), no matter what c is, it will go away.
Along with the indefinite integral, there is also the definite integral.
What is a definite integral?
A definite integral, in two dimensions, gives the area that exists under a curve between two endpoints.
For example, let us take the function f(x) = -x2+10 and the end points [-2, 2]. We could find the area under this curve using an indefinite integral.
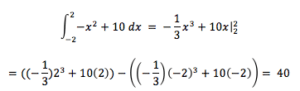
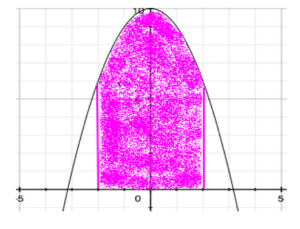
Integration is a very powerful tool that allows us to solve a wide range of problems. Check back soon to see our blog posts on how to determine various integrals, how to use our calculator to solve integration problems, and for practice AP integral problems.





Leave a Reply