We want to focus on the definite integral of a polynomial function. These arise very commonly in calculus, so here are detailed solutions to two problems, one multiple-choice and one free-response, involving a definite integral of polynomial.
Free-Response Definite Integrals:
You will not commonly be asked to evaluate common definite integrals on the free-response, but rather you will be asked to find an area or compute a volume, which will require computing a common definite integral. Suppose we want to compute the volume of the solid obtained by revolving the function 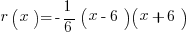 about the x-axis:
about the x-axis:
The cross sections when cutting perpendicular to the x-axis are circles with radius given by the function 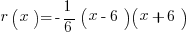 . The definite integral that needs to be evaluated is
. The definite integral that needs to be evaluated is 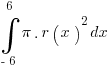 , since this is the area of a circle multiplied by the length of the interval from -6 to 6. We compute:
, since this is the area of a circle multiplied by the length of the interval from -6 to 6. We compute:
Therefore to compute the integral we compute the sum of the integrals of the individual terms, since polynomials are sums of continuous functions:
Recall the Fundamental Theorem of Calculus (FTC):
THEOREM: If v(x) is a continuous function with an antiderivative V(x), then 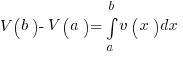 where , are in the domain of v(x).
where , are in the domain of v(x).
The FTC says that we can pick any old antiderivative V(x) for v(x), so we need to compute a string of antiderivatives for the integrands of the terms in the sum. In the previous post we discussed but did not state:
The Power Rule: The derivative 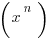 ‘=
‘=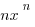
We used this to find that the integral 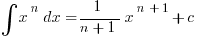 , and since we only need one antiderivative to evaluate definite integrals, we can take for use in this case.
, and since we only need one antiderivative to evaluate definite integrals, we can take for use in this case.
Therefore we can evaluate (using the fact that 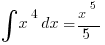 ,
, 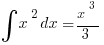 ,
, 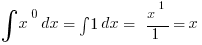 and the FTC):
and the FTC):
You can use your calculator to get 723.823 units cubed.
Multiple-Choice Definite Integrals:
Here is a sample of a typical multiple-choice question asking for you to formulate a definite integral based on the same concept discussed above.
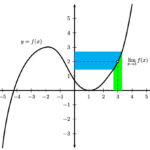
Question: A solid is generated by revolving the region enclosed by the function 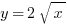 , and the lines x=2, x=3, y=1 about the x-axis. Which of the following definite integrals gives the volume of the solid? (Hint: Draw a picture)
, and the lines x=2, x=3, y=1 about the x-axis. Which of the following definite integrals gives the volume of the solid? (Hint: Draw a picture)
The idea for this problem is to recognize that this solid is a difference of integrals. Suppose that we had the volume of the function 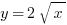 when bounded by the lines x = 2, x = 3, and rotated about the x-axis—then we would have the volume of the following solid:
when bounded by the lines x = 2, x = 3, and rotated about the x-axis—then we would have the volume of the following solid:
Given this volume, we would only need to subtract the volume of the following figure, derived by rotating y=1 bounded by x=2, x=3, about the x-axis:
From the upper volume, with radius 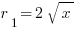 :
:
Therefore we need to subtract the two integrals, however using the integral laws we can express this in the form 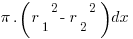 , which we follow up by substitution of our names for
, which we follow up by substitution of our names for 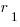 ,
,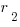 :
:
So the answer is A.
To compute the value of the integral we see that

This has the value 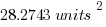 .
.













Leave a Reply