What are Riemann sums? A Riemann sum is a sum that estimates the value of a definite integral (or area under a curve if the function is positive). There are a number of different types of Riemann sum that are important to master for the AP Calculus BC exam.
We’ll cover the basics and see a few examples below.
Riemann Sums — Definition
Given a function f(x), and an interval [a, b], a Riemann sum estimates the value of the definite integral of f(x) from x = a to x = b according to the formula:
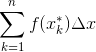
What Does it All Mean???
First of all, it’s important to know what all that notation means.
That big Greek letter Sigma (Σ) is an instruction to add up a bunch of terms.
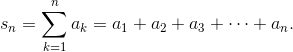
What follows the Σ are the terms that you will compute and add up.
Each term is an area calculation for a rectangle. As you know, the area of any rectangle is equal to its height times its width.
In the case of a Riemann sum, the heights are always function values:
![]()
On the other hand, the width is the same for each rectangle, and there’s a formula to find it:
![]()
Here, a and b are the given endpoints of the interval. (Equivalently, those are the bounds of integration in a definite integral.) The variable n stands for the number of rectangles in the Riemann sum.
We will also need to know about the points xk that serve to cut up the interval. Here’s a formula to find each one (just plugin in k = 0, 1, 2, …, n).
![]()
Now different kinds of Riemann Sums use these xk points in different ways. Although it seems like a lot to remember, the process is actually pretty straightforward. Try not to stress out!

Types of Riemann Sum
There are three basic types of Riemann sum that could show up on the Calculus BC exam.
- Right endpoint sum
- Left endpoint sum
- Midpoint Rule
Other, more advanced estimation formulas such as the Trapezoid Rule and Simpson’s Rule, are not technically Riemann sums. However, they are similar in spirit, and so we’ll talk about them as well.
No matter what, every method begins the same way.
- Find Δx.
- Find the points xk.
I like to put the points xk onto a number line. You should always have x0 = a and xn = b, as shown below.

Examples
Let’s estimate the value of ![]() , using Right endpoint, Left endpoint, and Midpoint Riemann sums with four rectangles.
, using Right endpoint, Left endpoint, and Midpoint Riemann sums with four rectangles.
Setup Steps
First, find the width Δx. Here, a = 1, b = 3, and n = 4 are given.
![]()
Next, find the points xk.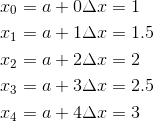
Right Endpoints
For the Right endpoint sum, ignore x0. The reason is that x0 is the extreme left point of the interval, and so it is not the right endpoint of any subinterval.
We will plug in the other points into the given function in order to find their heights. At this point, it helps to sketch the graph and understand where the right-endpoint rectangles are situated.
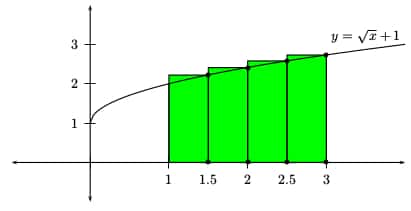
I like to organize my work into a table. There will be a column for the right endpoints, the heights and widths of each rectangle, and a final column for areas. Just multiply height × width to get area. Then add the numbers in the final column.
| Right Endpoints | Height: f(x) = √(x) + 1 | Width: Δx | Area |
|---|---|---|---|
| 1.5 | √(1.5) + 1 = 2.22 | 1/2 | 1.11 |
| 2 | √(2) + 1 = 2.41 | 1/2 | 1.21 |
| 2.5 | √(2.5) + 1 = 2.58 | 1/2 | 1.29 |
| 3 | √(3) + 1 = 2.73 | 1/2 | 1.37 |
| Total: | 4.98 |
The final answer is 4.98.
Left Endpoints
Once you have seen a Right Riemann sum, the Left Riemann sum will be super easy. The only difference is which x-values to use. This time, ignore the extreme right endpoint, xn.
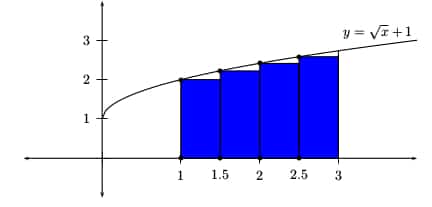
| Left Endpoints | Height: f(x) = √(x) + 1 | Width: Δx | Area |
|---|---|---|---|
| 1 | √(1) + 1 = 2 | 1/2 | 1 |
| 1.5 | √(1.5) + 1 = 2.22 | 1/2 | 1.11 |
| 2 | √(2) + 1 = 2.41 | 1/2 | 1.21 |
| 2.5 | √(2.5) + 1 = 2.58 | 1/2 | 1.29 |
| Total: | 4.61 |
This time, we get 4.61 as a final answer.
Midpoint Rule
Now for Midpoint Rule, we have to do an extra step.
Calculate the midpoints of each subinterval. There’s an easy formula to do this:![]()
So let’s find those midpoints in our example!
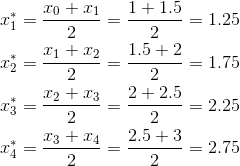
Here is what the Midpoint Rule looks like. Notice that each rectangle’s height is governed by where its midline hits the curve.
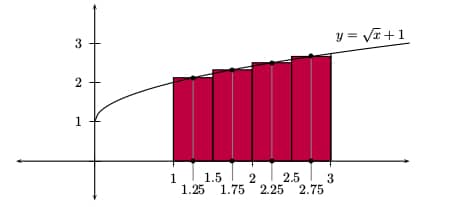
Now plug these midpoints into the formula (again, using a table).
| Midpoints | Height: f(x) = √(x) + 1 | Width: Δx | Area |
|---|---|---|---|
| 1.25 | √(1.25) + 1 = 2.12 | 1/2 | 1.06 |
| 1.75 | √(1.75) + 1 = 2.32 | 1/2 | 1.16 |
| 2.25 | √(2.25) + 1 = 2.50 | 1/2 | 1.25 |
| 2.75 | √(2.75) + 1 = 2.66 | 1/2 | 1.33 |
| Total: | 4.80 |
Here, the final answer is 4.8.
More Advanced Approximation Methods
Although the following methods are not really Riemann sums, they do fit the general pattern. First of all, both Trapezoid Rule and Simpson’s Rule involve sums of certain function values. Second, both methods estimate the value of a definite integral.
Let’s see how they work.
Trapezoid Rule
The Trapezoid Rule is so named because we use trapezoids rather than rectangles to do the approximation.
Without getting bogged down in the theoretical details, there is a formula that works out all of the trapezoid areas for you.
![]()
So, with our running example, the estimate using four trapezoids is: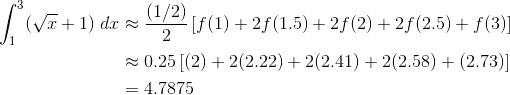
The final answer is about 4.788.
Simpson’s Rule
Simpson’s Rule is a much more accurate way to estimate the definite integral value. However, the formula is a little trickier.
For one thing, you must use an even number of subintervals. That is, n must be even.
![]()
Except for the first and last terms, the coefficients alternate between 4 and 2.
Here’s an example of using Simpson’s Rule:
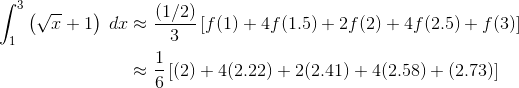
Working out this sum, you should get approximately 4.792.
Relationship to the Definite Integral
Finite Riemann sums only provide estimates. However, as the number of rectangles increases, the better the estimate will be.
In fact, in the limit as n → ∞, the Riemann sum converges to the exact area under the curve!
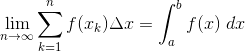
Fortunately you won’t have to work out this kind of limit on the exam. Instead, you can rely on more straightforward formulas specific to integration. See AP Calculus Exam Review: Integrals for more about that.





Leave a Reply