What is the Lagrange error bound? Basically, it’s a theoretical limit that measures how bad a Taylor polynomial estimate could be. Read on to find out more!

Taylor Series and Taylor Polynomials
The whole point in developing Taylor series is that they replace more complicated functions with polynomial-like expressions. The properties of Taylor series make them especially useful when doing calculus.
Remember, a Taylor series for a function f, with center c, is:
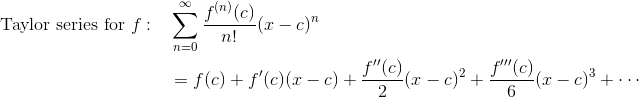
Taylor series are wonderful tools. However, the biggest drawback associated with them is the fact that they typically involve infinitely many terms.

So in practice, we tend to use only the first few terms. Maybe 3 terms, maybe 30, but at least a finite number of terms is more reasonable than all infinitely many of them, right?
But there is a trade-off. You lose accuracy. A Taylor polynomial (that is, finitely many terms of a Taylor series) can provide a very good approximation for a function, but it can’t model the function exactly.
That’s where the error comes in.
By the way, now would be a great time to review: AP Calculus BC Review: Taylor Polynomials and AP Calculus BC Review: Taylor and Maclaurin Series.
The Lagrange Error Bound
Let T(x) be the nth order Taylor polynomial for a given function f, with center at c.
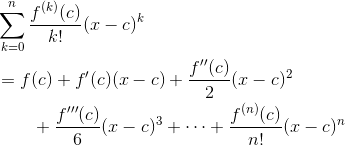
Then the error between T(x) and f(x) is no greater than the Lagrange error bound (also called the remainder term),
![]()
Here, M stands for the maximum absolute value of the (n+1)-order derivative on the interval between c and x. In other words, M is found by plugging in the z-value between x and c that maximizes the following expression:
![]()
That may sound complicated, but in practice, there’s usually a quick way to decide what M should be.
Example
Use the Lagrange error bound to estimate the error in using a 4th degree Maclaurin polynomial to approximate cos(π/4).
Solution
First, you need to find the 4th degree Maclaurin polynomial for cos x. A Maclaurin polynomial is simply a Taylor polynomial centered at c = 0.
![]()
Now, for the error bound, we’ll need to know what the 5th-derivative of f(x) = cos x is. (You probably would have computed all of the derivatives up to the 4th order when you constructed the Maclaurin polynomial for the function, anyway.)
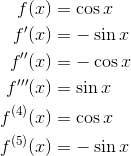
Now, the largest that |-sin x| could possibly be is 1. (Actually, we could do even better than that if we realize that |-sin(π/4)| = 0.707 maximizes the quantity on the interval [0, π/4], but we’ll stick with our first estimate of 1. After all, this is only an estimate!)
So, we have M = 1. Plugging this into the error bound formula with n = 4, we get:
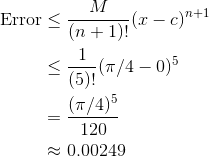
The error is roughly 0.0025
Follow-Up: How Good Was Our Estimate?
Because the computed error bound was so tiny, we can be sure that T(x) approximates the values of cos x incredibly well, at least when the input is within the interval from 0 to π/4.
Let’s compare values to see just how close the approximation really is. Computing each of T(π/4) and cos(π/4) to eight digits of accuracy:
![]()
![]()
The actual error is: 0.70742921 – 0.70710678 = 0.00032243. This is much better than our estimated error of 0.0025. Really, the Lagrange error bound is just a worst-case scenario in terms of estimating error; the actual error is often much less.





Leave a Reply