10 Most Common AP Calculus AB Mistakes (and How to Avoid Them!)

The AP Calculus AB exam is no walk in the park. The problems are challenging, and you really have to be on your toes to avoid errors. Here are the ten most common AP Calculus AB exam mistakes, and what you can do to avoid them.

Top 10 AP Calculus AB Exam Mistakes

In no particular order, here are the most common mistakes that I have seen students make on the exam.

1. Not Showing Work

This is probably the most common as well as the most serious mistake in the list.

As you know, the AP Calculus AB exam has a Free Response (FR) section. In order to score points for your answers, you must show your work.

Simply writing down a final answer is not good enough.

For more information about the Free Response section, check out these helpful tips to conquering AP Calculus Free Response questions

2. Crossing Out Good Work

Suppose you spent the last ten minutes furiously working out the solution to a free response problem, only to discover that your final answer doesn’t make sense. Maybe you feel like balling up the test paper and throwing it away. Relax, take a deep breath, and

DON’T ERASE OR CROSS OUT YOUR WORK!

Even if the answer is incorrect, your work may earn you partial credit. Every point counts on this exam, so leave all of your work for the graders to see.

3. Average Velocity is Not an Arithmetic Mean

When you see the word average on the AP Calculus AB exam, do start adding up things and dividing. Instead, the average velocity is a measure of change in position over change in time.

For example, if f(t) = t² is the position function for an object, then the average velocity on the interval [1, 3] is:

4. Forgetting the Constant of Integration

When you take an indefinite integral (antiderivative), you must tack on that “+ C” at the end.

This is especially important in initial value problems, where you must eventually solve to find the value of C.

5. Everything Distributes!

A very common mistake in beginning calculus students is to misuse the Distributive Law of algebra.

For example, we all know that 3(x + y) = 3x + 3y. That’s the correct context for distribution — multiplication distributes over addition.

But don’t go crazy and try to distribute other things that are not multiplication.

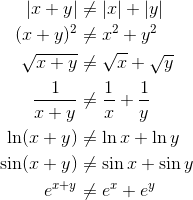
Some of the expressions in the list do simplify, but not by “distributing.”

For example, (x + y)² = x² + 2xy + y²,

and e^x+y = e^xe^y.

6. Omitting dy/dx in Implicit Differentiation

Implicit differentiation can be tricky. You have to remember that there are slightly different rules for x and y.

You have to treat an expression of y as if there is some unknown function in place of y. That means you’ll need to do a Chain Rule, and that’s where that extra factor of dy/dx comes in.

7. Parentheses Matter

In any formula in which you have to subtract a quantity, pay close attention to your grouping.

For example, suppose f(x) = x³ + 5, and g(x) = 2x² – 8. What is the expression for f – g?

If you said “x³ – 2x² – 3,” then unfortunately you’ve fallen into this common trap.

You have to subtract the entire expression for g, not just the first term. That means you’ll need a set of parentheses around g.

let’s see the correct way to do it.

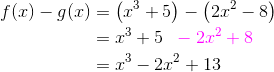
8. Natural Log is Not 1/x

I always put the following True/False question on my calculus tests.

The answer is False. The two expressions are not interchangeable.

Instead, the correct relationship is that one is the derivative of the other:

9. Integrals and Logarithms

Related to Mistake 8, we may know that the integral of 1/x is ln(x) + C. But this doesn’t mean that the integral of 1/f(x) would be ln(f(x)).

Usually, other techniques or rules must be used in those cases.

For example, ,

not:     ln(x² + 1) + C.

10. Forgetting to Use the Product Rule

Now I know if you’re taking an AP Calculus Exam, your teacher has drilled into your head the proper use the the product, quotient, and chain rules.

However, it’s easy to slip up on the test.

For example, if you are doing a related rates problem, and you have to find the derivative of r²h with respect to time t, then you must use product rule.

Conclusion

Hopefully after reviewing these 10 Calculus AB exam mistakes, you’ll be able to avoid them on the test!

Of course this list is not comprehensive. Find out what calculus errors you tend to make and take steps to correct them before the exam.