The Shell Method is a technique for finding the volume of a solid of revolution. Just as in the Disk/Washer Method (see AP Calculus Review: Disk and Washer Methods), the exact answer results from a certain integral. In this article, we’ll review the shell method and show how it solves volume problems on the AP Calculus AB/BC exams.
Solids of Revolution and the Shell Method
Briefly, a solid of revolution is the solid formed by revolving a plane region around a fixed axis.

We defined solids of revolution in a previous article, AP Calculus Review: Disk and Washer Methods. So you might want to read up before continuing.
Shells, Shells, and more Shells…
Suppose you need to find the volume of a solid of revolution. First we have to decide how to slice the solid. If you wanted to slice perpendicular to the axis of revolution, then you would get slabs that look like thin cylinders (disks) or cylinders with circles removed (washers). However, the Shell Method requires a different kind of slicing.
Imagine that your solid is made of cookie dough. And you have a set of circular cookie cutters of various sizes. Starting with the smallest cookie cutter and progressing to larger ones, let’s slice through the dough in concentric rings.
Making sure to slice in the same direction as the axis of revolution, you will get a clump of nested shells, or thin hollow cylindrical objects.

Approximating the Volume
Now let’s take a closer look at a single shell.
As long as the thickness is small enough, the volume of the shell can be approximated by the formula:
V = 2πrhw
Note that the volume is simply the circumference (2πr) times the height (h) times the thickness (w). In fact, you can think of cutting the shell along its height and “unrolling” it to produce a thin rectangular slab. Then the volume is simply length × height × width as in any rectangular solid.
Now suppose we have a solid of revolution with generating region being the area under a function y = f(x) between x = a and x = b. And suppose that the y-axis as its axis of symmetry. (This is the easiest case).
Finally, after taking the limit as n → ∞ (so that we have infinitely many shells to fill out the solid), we get the exact formula.
![]()
![]()
Example 1
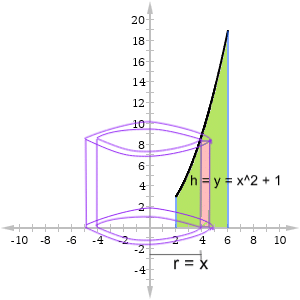
Find the volume of the solid generated by revolving the region under f(x) = x2 + 1, where 2 ≤ x ≤ 6, around the y-axis.
Solution
It might help to sketch a figure. Fortunately, this is exactly what’s pictured in the figure above.
First identify the dimensions of a typical shell.
- r = x
- h = f(x) = x2 + 1
- Thickness = dx
In addition, we use a = 2 and b = 6 because we have 2 ≤ x ≤ 6.
Now set up the Shell Method integral and evaluate to find the volume.
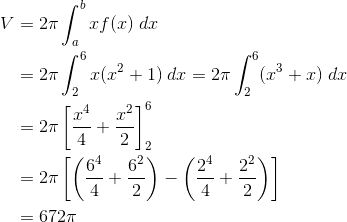
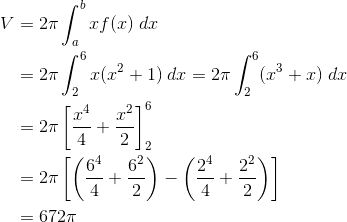
Thus the volume is equal to 672π cubic units.
More than One Function
When the generating region is defined as the area between two functions, then we have to modify the formula somewhat.
Consider the region between two curves, y = f(x) on top and y = g(x) on bottom, between x = a and x = b.
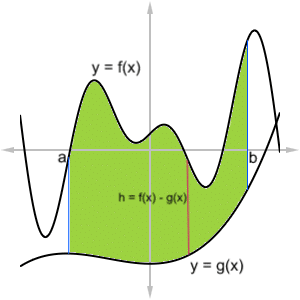

The height at a typical sample x-value is equal to the difference of the two function values. That is,
h = y2 – y1 = f(x) – g(x)
This observation leads directly to the following version of the Shell Method formula:
![]()
![]()
Revolving around Different Axes
There are also variations of the formula to cover cases in which the axis of revolution is not the y-axis. In all cases though, the axis must not be interior to the region itself.
Be careful! The horizontal axis cases require that the functions be solved for x rather than y.
- Vertical Axis x = h entirely to the left of the region bounded above by y = f(x) and below by y = g(x):

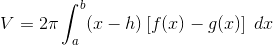
- Horizontal Axis y = k entirely below the region bounded on the right by x = f(y) and on the left by x = g(y):

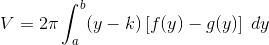
Example 2
Let R be the region bounded by y = x4 and y = 3x3. Find the volume of the solid generated by revolving R around the line x = -2.
Solution
Let’s make a sketch. There is only a tiny sliver of area between the two curves.
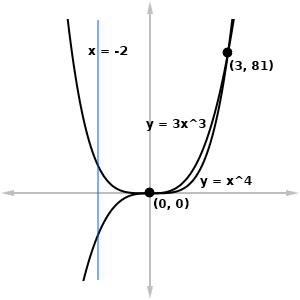

To find the bounds of integration, we need to set the two functions equal.
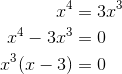
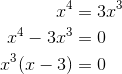
So we get x = 0 and x = 3. These two values will be our a and b in the integral.
Then identify the radius, height, and thickness of the typical shell.
- r = x – (-2) = x + 2
- h = f(x) – g(x) = 3x3 – x4
- Thickness = dx
Finally, put it all together and evaluate the definite integral.
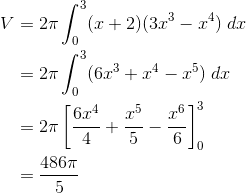
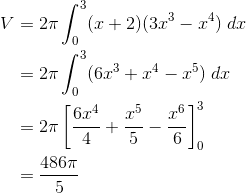





Leave a Reply