In calculus, we learn that the tangent line for a function can be found by computing the derivative. So there’s a close relationship between derivatives and tangent lines. However, they are not the same thing. For starters, the derivative f ‘(x) is a function, while the tangent line is, well, a line.
Instead, the correct statement is this: “The derivative measures the slope of the tangent lines.”
Think about this: a clock is not the same thing as time. But if you want to know the time of day, you can go look at a clock to find out. A clock measures the time at any particular point throughout the day.

Let’s take a closer look at tangent lines.
What is a tangent Line?
A tangent line for a function f(x) at a given point x = a is a line (linear function) that meets the graph of the function at x = a and has the same slope as the curve does at that point.
Sometimes we might say that a tangent line “just touches” the curve, or “intersects the curve only once,”f but those ideas can sometimes lead us astray.
The graph below shows the tangent lines (in red, purple, and magenta) at three different points on a curve y = f(x) (in black).
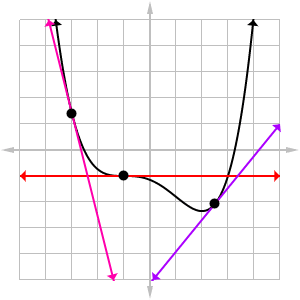
Slope and Derivatives
So how do we know what the slope of the tangent line should be? After learning about derivatives, you get to use the simple formula,
m = f ‘(a).
In this formula, the function f and x-value a are given. Your job is to find m, which represents the slope of the tangent line. Once you have the slope, writing the equation of the tangent line is fairly straightforward.
Finding the Tangent Line
Suppose you are asked to find the tangent line for a function f(x) at a given point x = a. Here is a step-by-step approach:
- Find the derivative, f ‘(x).
- Plug in x = a to get the slope. That is, compute m = f ‘(a).
- If not already given in the problem, find the y-coordinate of the point. As always, you plug the x-value into the function in order to get the y-value. Let b = f(a).
- Use the point-slope form and solve for y to find the equation of the tangent line. In other words, plug in your values of m, a, and b into the equation,
y = m(x – a) + b.
The Derivative Measures Slope
Let’s take another look at that first step, “Find the derivative.” Remember, the derivative is a function (of the input variable x). By plugging in different input values, x = a, the output values of f ‘(x) give you the slopes of the tangent lines at each point x = a.
This is what we mean when we say that “the derivative measures the slope of the tangent lines.”
If I want to know the slope of f at x = 1, then I compute f ‘(1). And if I want to know the slope at x = -352/13, then I compute f ‘(-352/13). Simple as that!
Example: A Polynomial
Now let’s look at an example function, f(x) = x3 + 3x2 + 1. We’ll find the tangent lines at a few different points.
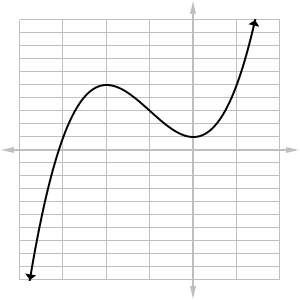
First of all, find the derivative: f ‘(x) = 3x2 + 6x. (for practice finding derivatives, check out this Magoosh article about derivatives).
The function value and derivative value at a few points are shown in the table below:
| x | -3 | -2 | -1 | 0 | 1 |
| f(x) = x3 + 3x2 + 1 | 1 | 5 | 3 | 1 | 5 |
| f ‘(x) = 3x2 + 6x | 9 | 0 | -3 | 0 | 9 |
For the points listed, we can easily find the equation of the tangent line. Note, on the AP Calculus Exam, the multiple choice answers may be simplified. So I’ve shown you both the point-slope form and the simplified, or slope-intercept, form of the tangent line.
| x | Tangent line, point-slope form | Tangent line, simplified |
|---|---|---|
| -3 | y = 9(x + 3) + 1 | y = 9x + 28 |
| -2 | y = 0(x + 2) + 5 | y = 5 |
| -1 | y = -3(x + 1) + 3 | y = -3x |
| 0 | y = 0(x – 0) + 1 | y = 1 |
| 1 | y = 9(x – 1) + 5 | y = 9x – 4 |
Now let’s see the graph of y = f(x) together with the tangent lines that we just found.
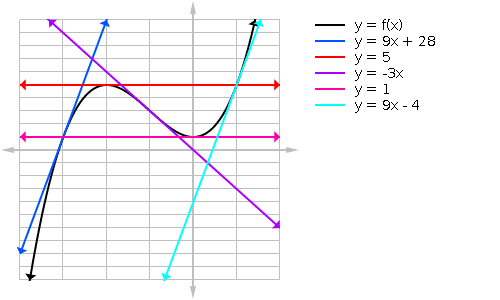
Summary
So now you know. The derivative is not the same thing as a tangent line. Instead, the derivative is a tool for measuring the slope of the tangent line at any particular point, just like a clock measures times throughout the day. With this in mind, you’ll have no trouble tackling tangent line problems on the AP Calculus exam!
For more about slope, tangent lines, and derivatives, check out these related Magoosh articles: Is the Derivative of a Function the Slope? and How to Find the Slope of a Line Tangent to a Curve.




Leave a Reply