AP Calculus Review: Trigonometric Identities

What are trigonometric identities doing on a Calculus exam? I’m glad you asked! Because mathematics tends to build upon previous results, you can expect to use all of your prior math knowledge when working on calculus problems.

Trigonometry is useful when setting up problems involving right triangles. Moreover, the trigonometric identities also help when working out limits, derivatives and integrals of trig functions. Specifically, these identities seem to come up more often when working out integrals, especially on the no-calculator sections of the test.

The Unit Circle

First of all, you should be familiar with the Unit Circle. Each point (x, y) on the circle gives the value of cosine and sine of the corresponding angle.

For example, look for the angle 2π/3 (radians). Based on the unit circle diagram, you know:

• cos 2π/3 = -1/2.
• sin 2π/3 = √ 3 /2.

The Essential Trigonometric Identities

Fortunately, you do not have to remember absolutely every identity from Trig class. Below is a list of what I would consider the essential identities.

1. Quotient Identities

The quotient identities are useful for re-expressing the trig functions in terms of sin and/or cos.

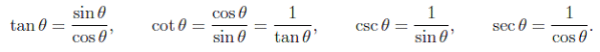
2. Even and Odd Properties

The following rules provide shortcuts for dealing with negative input.

3. Pythagorean Identities

Perhaps the most famous and useful equation in all of mathematics is the Pythagorean Theorem. If the side lengths of a right triangle are a and b, and the hypotenuse is c, then:

When applied to the unit circle, we get a trio of useful trigonometric identities:

4. Half-Angle Identities

The half-angle identities can be used to convert a squared expression into a form that is easier to deal with. So if sine-squared or cosine-squared shows up in an integral, remember these identities.

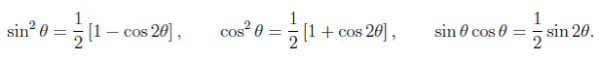
Examples

As you can see, the list of essential trig identities is not terribly long. In fact, there are just a few key items to remember. Now let’s see how we can use these identities in actual AP Calculus problems.

Using the Unit Circle

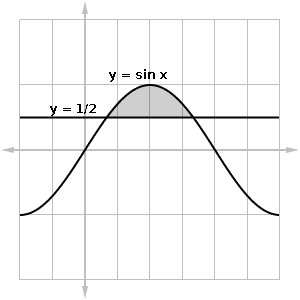
Find the area of the shaded region between y = sin x and the line y = 1/2.

Solution

We know that a properly set-up integral will do the trick. But what should the limits of integration be? We first have to solve sin x = 1/2.

Based on the unit circle, there are two angles at which the sine value is 1/2:    π/6 and 5π/6. Therefore, the area of the shaded region is:

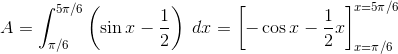
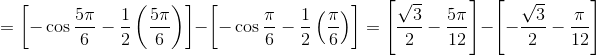
Note how we also used the unit circle at the end to determine the values of cos π/6 and 5cos π/6.

Using the Quotient and Pythagorean Identities

Solution

At first, this integral seems impossible! However with a bit of skillful manipulation, this one transforms into an easier problem.

First let’s re-express the division by cos² x as a multiplication by its reciprocal, sec² x.

Then notice that an additional sec² x can be factored out.

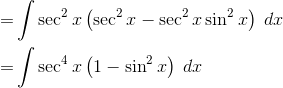
Next, we use a form of the Pythagorean identity.

Therefore, we can rewrite the integral as:

Notice the cosines and secants. As we know, those two trig functions are reciprocals of one another. So, just like 4 and 1/4 would cancel when multiplied together, we can cancel two of the cosines and secants. This leaves a very simple integral:

It may seem strange that after all of that work, the final answer is so trivial. But this is often the case when using trigonometric identities to manipulate the problem. Test makers are really good at creating problems that unravel like this.

Using Even and Odd Properties

Describe the vector function (cos(-t), sin(-t)), where 0 ≤ t ≤ 2π.

(A) A circle traced counterclockwise starting and ending at (1, 0)

(B) A circle traced clockwise starting and ending at (1, 0)

(C) A circle traced counterclockwise starting and ending at (0, 1)

(D) A circle traced clockwise starting and ending at (0, 1)

Solution

First, plug in t = 0.

(cos(-0), sin(-0)) = (cos(0), sin(0)) = (1, 0).

This rules out (C) and (D) immediately.

Next, the easiest way to determine the correct direction is to use the even and odd properties of sine and cosine.

cos(-t) = cos(t).

sin(-t) = -sin(t).

Therefore, the original vector function is equivalent to: (cos(t), -sin(t)). But this new path is simply a reflection of the original path over the x-axis, because the y-coordinate has been negated.

If you recall that (cos(t), sin(t)) traces out the standard unit circle counterclockwise, then (cos(t), -sin(t)) traces it out the other way, that is, clockwise.

The correct response is (B).

Using the Half-Angle Identities

Solution

The only way to proceed on this one is to use a half-angle identity. Just be careful with the 4x inside. You’ll have to multiply that by 2 in the formula.

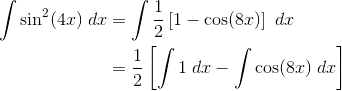
Let’s split up the work now. The first term is trivially easy.

But the second term requires a substitution. Let u = 8x. Then du = 8 dx, or equivalently, dx = (1/8) du.

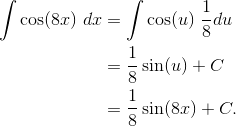
Putting these two results together with the main problem, we get:

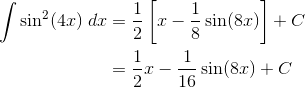
Summary

There are only a handful of trigonometric identities that you must master for the AP Calculus exams. Together with knowing your way around the unit circle, make sure that you understand when and how to use:

1. Quotient Identities
2. Even and Odd Properties
3. Pythagorean Identities, and
4. Half-Angle Identities