AP Calculus Review: Improper Integrals

What’s so improper about improper integrals? Well maybe that term is a bit too harsh.

Just as an improper fraction takes a bit more work to change it into a more reasonable form, an improper integral is a kind of definite integral that simply takes a bit more care to work out. The term improper refers to infinite behavior — either involving infinite limits of integration or functions that themselves become infinite.

In this article we explore the concept of improper integrals, learn how to compute them, and discuss their interpretations. Before delving into this concept, you might want to refresh your integration skills by checking out: AP Calculus Exam Review: Integrals.

What are Improper Integrals?

An improper integral is a special kind of definite integral,

There are basically two ways in which the integral can be improper.

1. If the integrand f(x) becomes infinite at one or more points in the interval [a, b].
2. If either limit of integration is infinite, that is, if a = -∞ or b = ∞ (or both).

It is possible that an integral may involve both of the previous issues, but you almost certainly will not see one so complicated on the AP Calculus exams. It’s also worth noting that improper integrals appear only on the BC test, not the AB.

Infinite Integrands

Suppose f is a function that is continuous on the open interval (a, b). Now if f becomes infinite at either a or b, in other words, if either of the following limit statements are true,

then the integral is improper at a, or b, depending on which one has the infinite behavior.

In order to evaluate the integral, we must set up a limit problem.

Example 1

For example, the function      has an infinite limit as x → 0 from the right.

Therefore, the integral below is improper.

In order to evaluate the integral, we treat it as a limit problem. Instead of the constant 0 (at which f is undefined), replace the lower bound with a variable a. Then use the limit notation to indicate that a → 0. However, we must wait until after anti-differentiation before attempting to take the limit.

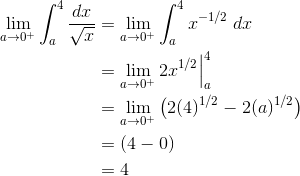
Note, the only time we had to worry about the limit was at the very end when we plugged in the limiting value, a = 0.

Infinite Integrand but Finite Area?

So what does the value of 4 mean in the previous example? If we recall the geometric interpretation of the definite integral as the area under the function, then we run into a little trouble as we near x = 0. Because the values of f get larger and larger without bound, shouldn’t the area under y = f(x) also get infinite?

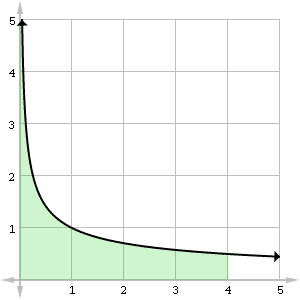
This is one of the many great paradoxes that mathematics has to offer. Even though the values of a function become infinite, the total area under that function may still remain finite!

In the above example, we can say with full confidence that the area under , between the y-axis and the line x = 4, is exactly 4 square units. Just think of the infinite “spike” near x = 0 as getting so incredibly thin as you travel higher and higher that its contribution to the total area is insignificant.

Infinite Limits of Integration

If one or both of the limits of integration is infinite, then we call the integral improper as well. There are three situations:

In fact the third situation must be split up into two integral anyway, so there are really only two situations.

1. The lower limit (a) is -∞, or
2. The upper limit (b) is ∞.

Both scenarios are handled by replacing infinity with a variable and taking the limit after integrating.

Example 2

Find the value of .

First replace ∞ by a variable, such as b. Then work out the integration, and finally determine the limit as b → ∞.

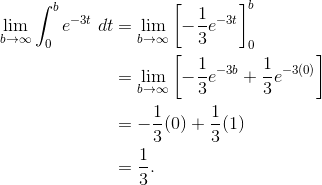
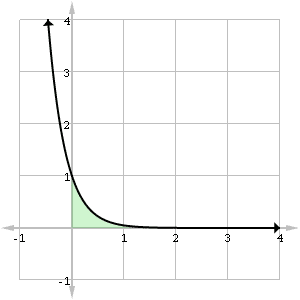
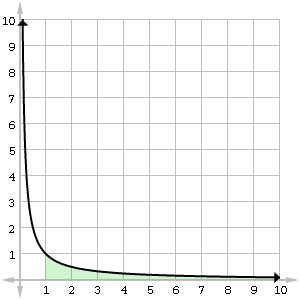
The graph below shows the area shaded. Because the integrand function e ^-3t approaches zero so quickly, it may be easier to believe that there is only a total area of 1/3 under the curve on the interval [0, ∞).

Divergent Improper Integrals

Not every improper integral converges, or works out to a finite numerical value. Sometimes the limit fails to exist (becomes infinite), and in these cases we would say that the integral diverges.

Example 3

Setting this improper integral up as a limit, we find:

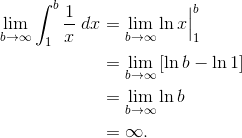
Because the limit is ∞, we conclude that this improper integral diverges. In fact this is a famous integral, and it may be surprising that this one diverges even though the values of 1/x tend toward 0 as x → ∞. The area under that graph is actually infinite this time!

Example 4

At first, this definite integral may not look improper. But upon closer inspection, we realize that sec θ is undefined at the endpoint, θ = π/2. In fact,

Now this doesn’t imply that the integral diverges, just that we must be careful in evaluating it. Let’s set up the improper integral as we have above — as a limit.

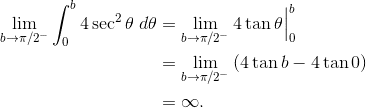
Thus the improper integral diverges, because the limit of the antiderivative ends up being infinite at π/2 as well.

Summary

• Improper integrals come in two main types.
  1. The integrand becomes infinite at one or more points in the interval.
  2. Either limit of integration (or both) is infinite.
• To evaluate an improper integral, first set it up as a limit that avoids the infinite behavior. Then find the antiderivative, and finally take the limit.
• If the value of the improper integral is finite, then it converges. Otherwise, the integral diverges.