AP Calculus Exam Review: Integrals

The AP Calculus Exams include a substantial number of problems involving integrals. In this short review, you’ll see the major topics that you’ll need to be aware of.

What is an Integral?

There are two kinds of integrals, the indefinite and definite integrals. They differ in many ways, however the notation is almost the same.

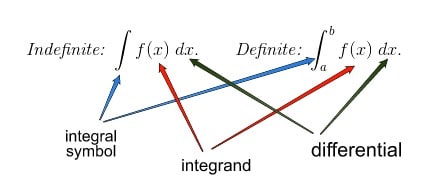
The numbers a and b in the definite integral notation are called the limits or bounds of integration.

Indefinite Integrals

An indefinite integral is another name for the antiderivative. In fact, the indefinite integral stands for every possible antiderivative! That’s where the ” + C ” comes in.

Here, the function F is an antiderivative for f. That is, F ^‘(x) = f(x). For example, F(x) = x² is an antiderivative for f(x) = 2x, since (x²)’ = 2x.

Don’t Forget the ” + C “

But there are many other antiderivatives! Because the derivative of any constant is 0, it’s also true that (x² + 1)’ = 2x, or (x² – 65.32236)’ = 2x.

Therefore, the most general antiderivative of 2x would be x² + C, where C is an as-yet-undetermined constant.

This is why you always tack on that ” + C ” at the end of your answer.

Finding Antiderivatives

Now let’s talk about finding that function F(x). That’s the hard part. There are various rules and formulas that can help to find the integral (antiderivative). Perhaps the most important rules include the Power Rule and the rules for breaking down sums, differences, and constant multiples.

For example, these rules allow you to integrate any polynomial. Let’s see an example:

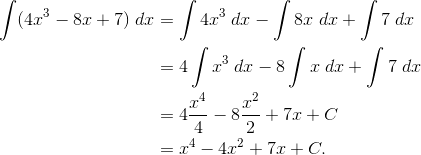
Notice near the end, we used ∫ 7dx = 7x. This is because the derivative of 7x is equal to 7. It works the same way for any constant term.

More Formulas?

There are many more integral formulas, techniques, and methods that you must master to score high on the AP Calculus Exam. For more information, check out this list of basic antiderivative formulas as well as this detailed review of integration techniques.

Definite Integrals and the Fundamental Theorem of Calculus

Definite integrals measure the area under a curve (among other things). The limits of integration, a and b, specify the left and right boundaries for the area under the graph of f(x) and above the x-axis.

To evaluate a definite integral, use the Fundamental Theorem of Calculus:

In this formula, F is the same thing it was before: an antiderivative for f. So the process goes like this:

1. Find an antiderivative for the integrand, using basic formulas and/or other techniques such as substitution, integration by parts, etc.
2. Plug the upper limit (b) and lower limit (a) of integration into the antiderivative F.
3. Subtract to find the final answer: F(b) – F(a).

An Example Definite Integral

Find the area under y = 9 – x² between x = -1 and x = 2.

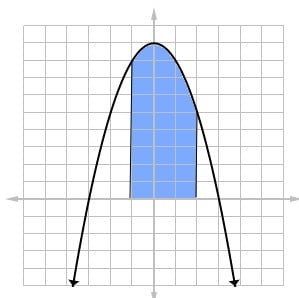
We first must set up the problem as a definite integral. Then evaluate the integral to find the area.

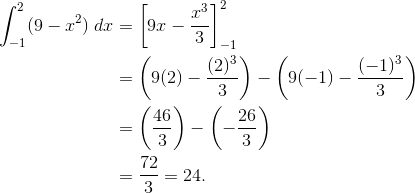
Net Area

Disclaimer: The idea of “area under a function” really only makes sense if f(x) ≥ 0 on the interval. In fact, it’s more correct to say that the definite integral computes the net area — that is, area above the x-axis minus area below the x-axis.

Here’s an example, using only the concept of net area to solve the integral problem.

Find , based on the graph below.

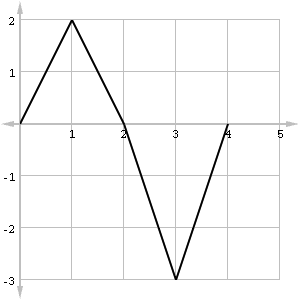
How in the world can we evaluate the integral if we’re not even given a formula for f(x)? Well, we are given the graph. This problem relies on our ability to interpret the definite integral as a net area.

Just find the area of each triangles. Remember, A = (1/2)bh.

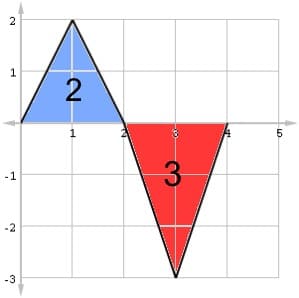
The triangle above the axis counts as positive, while the one below the axis counts as negative.

Therefore, the final answer is: 2 + (-3) = -1.

Applications of Integrals

Not only is it essential to know how to compute integrals, but you also must know what they’re good for. We’ve already talked about definite integrals and area. Here are a few additional applications that you should be aware of.

Position, Velocity, and Acceleration

If s(t) is a position function, then you know from differential calculus that the derivative, v(t) = s ‘(t) is the velocity function. Moreover, the second derivative, a(t) = s ”(t) is the acceleration function.

You can use integrals to go the other way. In other words, if you are given acceleration, you can find a velocity function, and if given velocity, then you can find a position function.

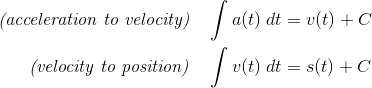
Typically further information may be required to nail down exactly what the appropriate constants are.

Length of a Curve

The length of a curve y = f(x) between x = a and x = b may be computed using the following definite integral.

Volume of Solids of Revolution

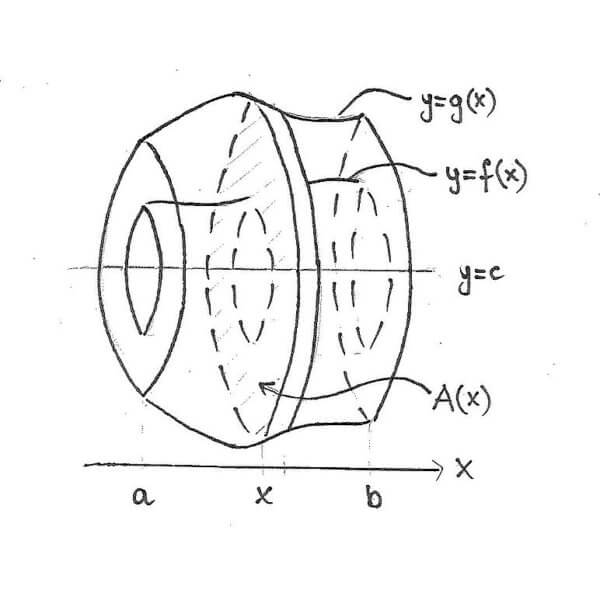
Solids of revolution can be quite tricky. However, it’s good to know that definite integrals are just the right tool for computing their volumes. The basic formulas are as follows:

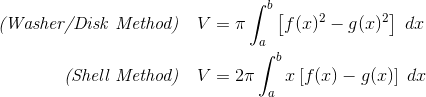
Summary

There are many topics related to integrals on the AP Calculus Exams. Each topic requires practice and study, but hopefully this review will get you started. Remember the key points:

• The indefinite integral of a function is the (most general) antiderivative of that function.
• There are numerous integral formulas to learn, including the Power Rule, rules for special kinds of functions (such as trigonometric and exponential), and more advanced techniques like substitution, integration by parts, and others.
• Definite integrals can be used to find net area.
• To evaluate a definite integral, either use the Fundamental Theorem of Calculus, or use geometric formulas to compute the net area directly.
• The Fundamental Theorem of Calculus states that a definite integral of a function is found by plugging the limits of integration into an antiderivative for that function, and then subtracting.
• There are a variety of important applications of integrals, including position/velocity/acceleration problems, curve/arc length, and solids of revolution.