Did you know that the majority of ACT test-takers find the Math Test to be the hardest section on the exam? It’s true: ACT Math can look off-putting at first glance. But it doesn’t have to be a struggle. With these 15 key concepts to review for ACT Math, you have your road map to ACT Math success!
A few notes:
- These topics are listed in order of their importance on the ACT Math Test. The topics at the bottom of the list may only show up in a handful of questions, but mastering them can make the difference between a score you’re happy with and one you wish you could change.
- This list is not exhaustive. In other words, it doesn’t cover all Math topics that appear on the ACT Math Test. These topics are those that students either find the most difficult, or ‘fall through the cracks’ as students prepare for test day. For a list and resources covering every single topic on the ACT Math test, check out our ACT Math posts!
Pre-Algebra (20-25%)
1. Mean, Median, and Mode
Ah yes: mean, median, and mode. They’re simple concepts to learn, but you don’t want to get them mixed up on test day.
- Mean: the average of all the numbers.
- Median: the middle value of a list of numbers.
- Mode: the number that appears most in a list. Remember, you can have more than one mode in a set of numbers!
2. Probability
If you want the odds to be in your favor, there’s one big rule to remember about probability.
- To determine probability, divide the number of particular outcomes by the number of total outcomes. Got three red candies in a bag of ten candies? That means you have a 30% chance of pulling a red candy out of the bag.
3. Absolute Value
If you see a vertical lines on either side of a number, that’s absolute value. If those lines are around a negative number, treat the number like a positive number as you solve an equation.
Elementary Algebra (15-20%)
4. Writing Expressions and Equations
From time to time, you will come across a word problem that contains an algebraic expression or equation. When you see one of these questions, have your pencil out and ready to underline this key information.
5. Multiplying Binomials
You may know this one as FOIL (First Outer Inner Last). Though easy with a little practice, double check your work, especially if there are one or more negative numbers involved.
6. Inequalities
The main thing to remember as you practice inequalities is that you should treat them like any other equation. THE ONLY DIFFERENCE is that when you multiply or divide by a negative number, switch the sign!
Intermediate Algebra (15-20%)
7. Relationships between the Sides of an Equation
If you’re having trouble figuring out the relationships between the sides of an equation, here are two things to remember.
- If multiplication (or squaring) is involved, the two sides of the equation will both go up.
- If division (or square roots) is involved, the two sides of the equation have an inverse relation. One will go up and the other will go down.
8. Functions
First of all, if you see ‘f(x)’, don’t freak out. ‘f(x)’ is no different than ‘y’ in an equation. And if you see a compound function, like (f(g(x)), it’s time to plug and play. But instead of plugging a number into a function, you’re plugging one function into another function.

9. Logarithms
Now, these are pretty rare on the ACT. Even so, they’re important to know, no matter what your score goal. Logarithms are the inverse of exponential functions. That may sound scary, but it’s surprisingly easy to remember after studying an example and applying the same rules to a few practice problems.
Coordinate/Plane Geometry (20-25%)
10. Conic Sections
These questions will test your knowledge of parabolas, ellipses, and circles.
- Parabolas: These ‘u’ shaped curves open either downwards or upwards. Parabolas are the visual representation of the quadratic formula.
- Circles: To figure out the equation for a circle, you need to know the radius and the location of the center of the circle.
- Ellipses: If attempting to match the graph of an ellipse to the correct equation (or vice versa), make sure to pay close attention to the center of the ellipse. The center, represented as (h,k) on the equation, is one of the first things to look for as you eliminate potential answer choices.
11. The Equation of a Line
Good ole’ y=mx+b. ‘m’ is the slope of your line, and ‘b’ is the y-intercept.
- The initial setup of some equations will be more complicated than y=mx+b. If this is the case, it is your job to simplify the equation so that ‘y’ is by itself on one side of the equation.
12. Simple Three-Dimensional Geometry
On some questions you will be asked to find the surface area, volume, or diagonal length of a cube or other rectangular solid/prism. Here are a few quick equations and tricks to remember.
- Surface Area for Cube: length x width x 6. You multiply by six because a cube has six sides.
- Surface Area for a Rectangular Solid: You have to do two different equations.
- For the end sides of the solid, multiple length by width. Multiply this number by two.
- For the longer sides, multiply length by width. Multiply this number by four.
- Add the two numbers together to determine the surface area of the solid.
- Volume: For any rectangular solid, there is only one way to find the volume. Volume = length x width x height.
- Diagonal Length: Just like with volume, you need to know the length, width, and height. Once you have those numbers, the equation to find diagonal length is easy: D = √(w² + l² + h²). Don’t forget the correct order of operations: square l, w, and h separately, add up the results, AND THEN take the square root!
Trigonometry (5-10%)
13. SOHCAHTOA
SOHCAHTOA is a great mnemonic device to remember how to calculate the sine, cosine, and tangent of any triangle.
- SOH: Sine = Opposite over Hypotenuse
- CAH: Cosine = Adjacent over Hypotenuse
- TOA: Tangent = Opposite over Adjacent
14. Solving Triangles
Applying your SOHCATOA knowledge to a triangle, it is possible to solve for ‘x’ when ‘x’ is the unknown length of one of the triangle’s sides.
- To make this even easier process, commit some time to memorizing the Sine, Cosine, and Tangent values for the following angles: 0, 30, 45, 60, and 90. Though this will take some brain power (and possibly a few flashcards), being able to plug in these values to an equation will save you a significant amount of time on the Math ACT Test. And if you’re shooting for a perfect 36 on the ACT, this is something you cannot afford to miss.
15. Trigonometric Graphs
Okay, to correctly answer the 1-2 questions concerning trigonometric graphs, you need to memorize the three graphs that represent the following equations.
- Y = sin x
- Y = cos x
- Y = tan x
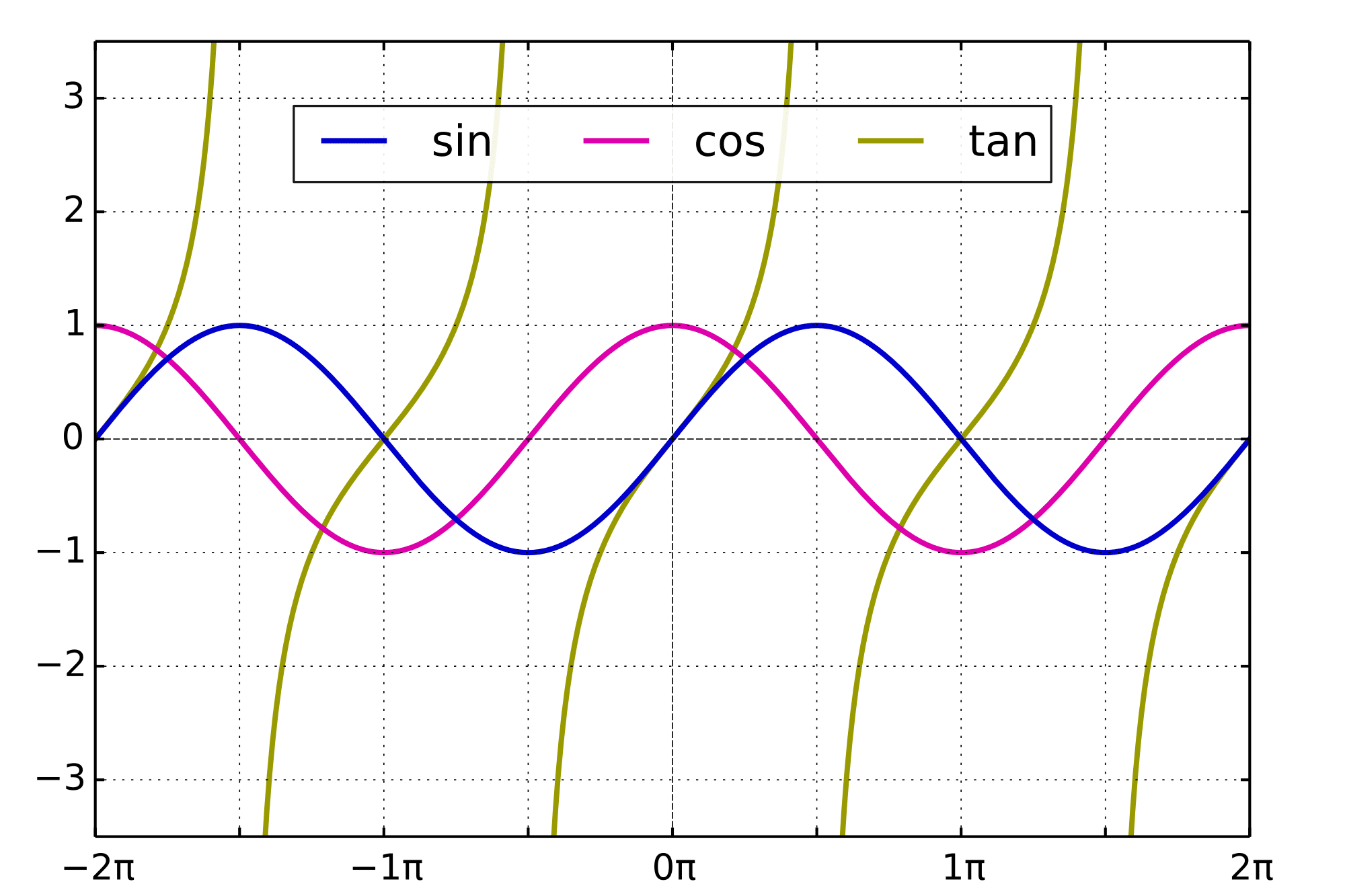
Now, if you know what these graphs look like in their simplest forms, it becomes a lot easier to match an equation to graph, even if the equation represents a graph where the amplitude or period has been stretched. As you go through examples, you will discover that matching a graph to the right equation (or vice versa) becomes surprisingly easy.
Final Thoughts
Well, Magooshers, I hope this article has helped you refresh some crucial Math topics. I certainly had a few flashbacks to high school Math classes while writing it. No matter which Math topics stump you, focus on your weaknesses as you prepare for test day (ratios giving you trouble? Here’s how to solve them!). Apply your newly-honed skills to practice problems before sitting down to a full-length practice test. If you do that, you are on your way to ACT Math Test success!





