Here is a quiz based on math concepts covered over the last month on the Magoosh GRE blog. See how many of the following five questions you can answer correctly in less than 8 minutes. Go!
1. Which of the following is a multiple of 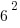 ?
?
(A) 36,045
(B) 43,623
(C) 52,224
(D) 89,892
(E) 92,044
2. To graduate John needs to complete eight courses. Of these eight, he must take only three science courses, only two math courses, and only one history course. If the college offers five science courses, six math courses, and four history courses, how many different class schedules can John have if the college offers a total of twenty courses?
(A) 150
(B) 600
(C) 3000
(D) 6000
(E) 12450
3.
| Column A | Column B |
| The sum of the multiples of 4 less than 100 | The sum of the multiples of 5 less than 100 |
(A) The quantity in Column A is greater
(B) The quantity in Column B is greater
(C) The two quantities are equal
(D) The relationship cannot be determined from the information given
4.
| Column A | Column B |
| The number of pentagons that can be inscribed in an octagon | The number of triangles that can be inscribed in an octagon |
(A) The quantity in Column A is greater
(B) The quantity in Column B is greater
(C) The two quantities are equal
(D) The relationship cannot be determined from the information given
5. A “trio-prime” is any number made up of three factors, not including itself and 1, that are consecutive primes. How many “trio-primes” are less than 1,000?
(A) 2
(B) 3
(C) 4
(D) 7
(E) 11
Answers:
1. D
2. D
3. A
4. C
5. B
Explanations:
1. I never talked about divisibility rules of 36. No test prep strategy would ever address such a random concern. Based on what you know, you have to be able to figure out how to answer this question.
We know divisibility rules of 6. But, that doesn’t really help us here. We have to think about this problem from a different angle: 36 can also be broken down into 9 and 4. In a previous post, I covered divisibility rules for both of these numbers. To determine which one of the answer choices is divisible by 36, I have to make sure that it passes the divisibility test for 9 and 4.
The rule for 9 is, if the sum of the digits of the number is a multiple of 9. The rule for 4 is, the last two digits should be divisible by 4. Only answer (D) fits both these requirements:
8+9+8+9+2 = 36
92/4 = 23
2. We must use the combination formula here for the three different classes. For science, John has 5C3 = 10, for math 6C2 = 15, for history 4C1 = 4. We multiply these results together- 10 x 15 x 4 = 600. The twist is, John has two other courses to take. If the college offers a total of 20 courses, John already has chosen from a total of 5+6+4 = 15. So, he only has 5 classes left or 5C2 = 10. Therefore, he has 600 x 10 = 6000 possible schedules. Answer (D).
3. Your first instinct may be to think that 5 is greater than 4, so the sum must be greater. However, there are more multiples of 4 under 100 than there are multiples of 5. You can write out the first few multiples for each, and see that 4 is already bigger than 5. Extrapolating this all the way to the multiple closest to 100, you can see that the sum of the multiples of 4 will be much bigger than the sum of the multiples of 5.
4. This question may look intimidating, but it is actually very straightforward. When we are figuring out how many smaller shapes (i.e. shapes with fewer sides) can be inscribed in large shapes (i.e. shape with more sides), we only need to use the combinations formula. For Column A, we get 8C5; for Column B, we get 8C3. These two values are equal. Therefore, the answer is C.
5. The only trio-primes are 2 x 3 x 5 = 30, 3 x 5 x 7 = 105, and 5 x 7 x 11 = 385. Answer B. If you chose answer C, remember that 7 x 11 x 13 yields 1001, which is too great by a hair.






Leave a Reply