Today, we’ll quickly look at how a rectangle and parallelogram can have the same area.
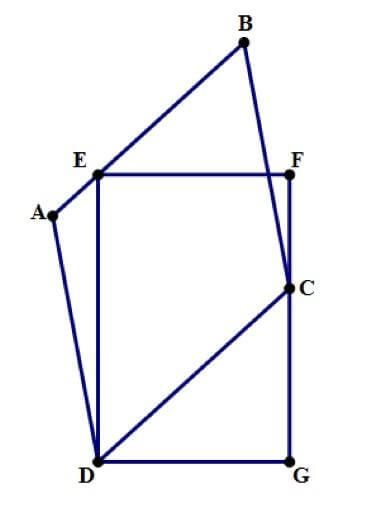
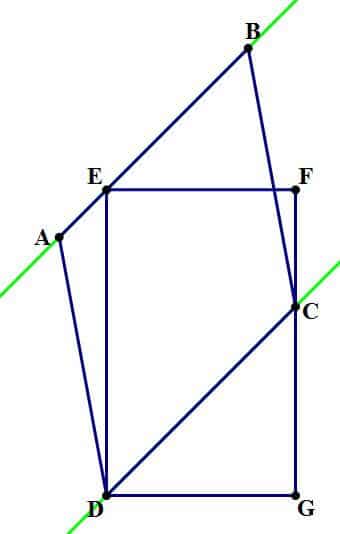
In the diagram to the above, the parallelogram and rectangle share a vertex (D), one vertex of the rectangle (E) is on a side of the parallelogram, and one vertex of the parallelogram (C) is on a side of the rectangle. That is enough information to guarantee that the rectangle and parallelogram have equal area.
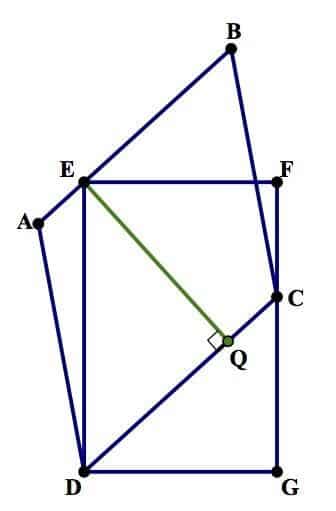
Here’s an argument why. In the diagram below, notice I have constructed segment EQ, which is perpendicular to CD. This segment is the height of the parallelogram, so that times the length of CD would be the area of the parallelogram.
Look at ΔDGC and ΔEQD. Those two triangles are similar. Why?
Well, first of all, ∠QDG and ∠EDQ are complementary: they both add up to the 90° angle of ∠EDG. Also, ∠QDG and ∠QCG are complementary, because they are the acute angles of a right triangle. Since ∠EDQ and ∠QCG are both complementary to the same angle (∠QDG), they are congruent: ∠EDQ≅ ∠QCG.
Since we know ∠EDQ≅ ∠QCG and we know ∠EQD≅ ∠G (both right angles), we know two angles in ΔDGC are congruent to two angles in ΔEQD. By the AA Similarity Theorem, they must be similar triangles.
ΔDGC ~ ΔEQD
Similar triangles have proportional sides. In particular, we can set up a proportion:
After cross-multiplying, we get two equal products. (ED)*(DG) = the area of the rectangle. (EQ)*(DC) = the area of the parallelogram. Therefore, those two areas are equal.
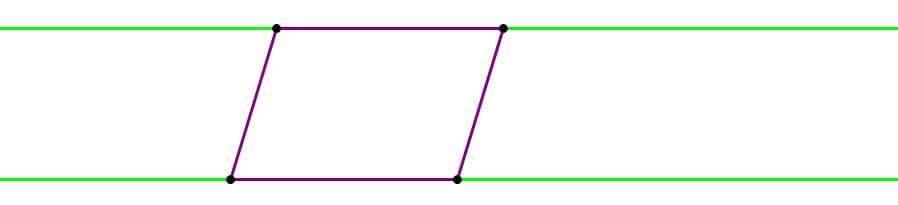
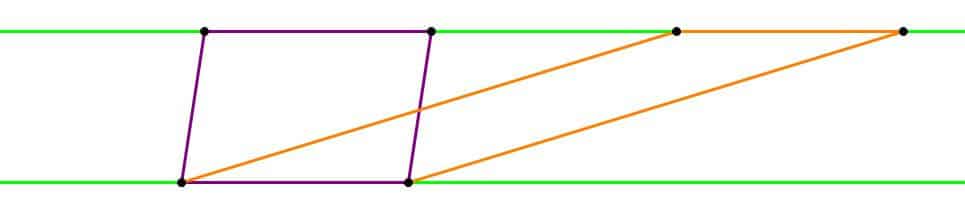
That’s a more equation-based way of proving the areas equal. Here’s another HUGE idea, which is much more appealing for visual thinkers. Imagine extending one pair of sides in a parallelogram like railroad rails:
If we slide either side along its “rail”, the shape of the parallelogram will change, but the area will stay the same, because the base (the length on the rail) doesn’t change, the height (the distance between the parallel lines) doesn’t change.
The purple and the orange parallelograms must have exactly the same area. That’s a HUGE geometry idea.
Now, think about our diagram, with some “rails” added.
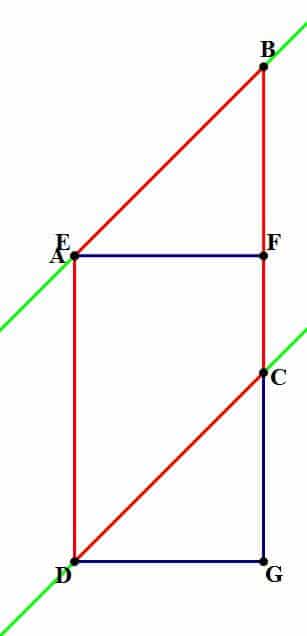
Now, when we slide AB upward, so that A coincides with E, that will make both AD and BC perfectly vertical:
Now, if we slide BC down, so it exactly coincides with FG, then the parallelogram will exactly coincide with the rectangle, which means they must have identical areas.
This “sliding method” can be a very handy shortcut with parallelogram areas.

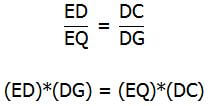





Leave a Reply