For some this is the most “interest”ing concept on the Revised GRE (at least for those with a fondness for bad puns). For most, compound vs simple section can be a nuisance. Many think, what is the difference between the two, and/or how did that formula go again?
But remember, this concept involves money, and for many that means its practical (especially if you invest money yourself). But enough rambling…
Simple Interest
Principal: The Amount of Money initially invested
Interest Rate: The amount return on an investment expressed as a percent of the principal.
Time: The length of time in which a principal is invested
Sample Problems
1. John invests 100 dollars in account that yields 8% simple interest annually. How much money will John have in his account after one year?
(A) $4
(B) $8
(C) $104
(D) $108
(E) $110
2. Bob invests 100 dollars in a fund that yields 15% simple interest monthly. If Bob invests the principal in the middle of January, which is the first month will he have more than $200 total?
(A) June
(B) July
(C) August
(D) February
(E) March
3. In 2001, John invests x dollars in a special account that yields y simple interest annually. If he has $250 in his account in 2006 and in 2008 he has $270 in his account, what is x + y?
(A) 5
(B) 25
(C) 200
(D) 205
(E) 210
Answers:
1. D
2. C
3. D
Compound Interest
Okay, that was the easy part. Now for compound interest. In compound interest things become complicated. We no longer have a nice, clean linear increase. To illustrate:
If Mike invests $100 at 10% simple annual interest, he will have $110. After two years he will have $120. That is his money grows by $10 every year. After 10 years, Mike will have doubled his money.
Now, let’s say Mike’s friend Thomas invests $100 at a 10% rate that is compounded annually. After one year, Thomas will have made the same amount as Mike. But then things start diverging. Remember how Mike always gets 10% of the original 100 (the original 100 is called the principal)? Well, Thomas – because things are getting compounded annually – gets 10% of whatever the value of the account is at the end of the year. Let’s see how this plays out over time.
1st year: 10% of 100 = 110
2nd year: 10% of 110 = 121
3rd year: 10% of 121 = 133.10
4th year: 10% of 133.00 (rounding down) = 146.30…
After 10 years, Thomas will have made $260, which is $60 more than Mike.
Okay, that may all seem like chump change, but the same percent increase applies to numbers with a few more zeroes thrown in. How would $260,000 vs. 160,000 sound?
Of course the point of this lesson is to understand the conceptual difference between the two forms of interest—and not to have you running to the nearest ban, since the numbers above are very generous.
Now for the fun part: Notice how, in the case of Thomas, I seemed to be doing mathematical wizardry. After all, how did I know that 10% compounded annually at 10 years is going to yield 160% of the principal? Well, let’s meet the formula:
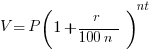
V = Total Value
P = Principal
r = annual interest rate
n = number of times per year invested
t = number of years
Pretty unpleasant, no? Well, let’s try to put the formula to the test. And you may want to get your calculators out (this is the Revised GRE after all!)
If $10,000 is invested at 10%, compounded semi-annually, how much will the investment be worth after 18 months?
(A) 11,500
(B) 11,505
(C) 11,576.25
(D) 11,625.30
(E) 12,000.50
Now don’t worry about the semi-annual bit—it just means twice a year. And remember the n from the scary little formula above: the number of times per year invested. And that 18 months? That corresponds to t, the number of years, which translates to 1.5.
.
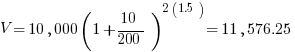That was easy—once you know where to put everything (and provided you remember the formula)!
Hi Chris,
concerning the first sample problem the answer should be 100$ as the interest is collected annually, i.e. the interest is only added to the whole year and not fractions of it by definition of simple interest, otherwise you will need to define the compounding rate.
thank you.
Oh yes, that’s right! Thanks for catching that
. I’ll make the necessary changes.
Chris you are going to kill me
what I said was wrong to some extend, I confused the mathematical definition of the word simple interest and compound interest and the collecting rate , i.e it’s ok to collect the simple interest per any period of time (a year or a fraction) as long as he didn’t mention in the question a certain collecting rate ( a constrain that a bank can add or something) I’ll use your example to explain my point
e.g. John invests 100 dollars in account that yields 8% simple interest annually, collected annually, How much money will John have in his account after 26 month?
the answer is 16$
on the other hand if it was 8% compound interest, with a monthly compounding rate, with an annual collecting rate then the answer is
100 x ((1+(0.08/12))^(12 x 2) = 117.288$
I’m sorry for that slip, I wasn’t accurate at all in what I wrote the first time, and I assumed that the interest is collected annually out of the blues I guess
Hi Amr,
Not a problem. Now I understand what you mean
. Sure, you can have all sorts of different non-yearly intervals with simple interest. It shouldn’t affect anything – the way it does with compound interest.
For the first compound interest problem, is there a faster way to calculate the exponent rather than multiplying it by itself multiple times? It seems rather time consuming
Hi Ben,
Actually, there is not a way that I know of. The good news is that with the calculator it is not that time-consuming. Anyhow, explanations of a concept can often time make the actual solution seem longer than it really is when you are simply punching the numbers into the calculator. One alternative though, if you don’t use a calculator, is to look at the answer choices. Usually two are three of them will not match with the numbers given in the question (e.g., round numbers when the answer clearly calls for a decimal).
Hope that helps
.
Thanq very much chris giving good stuff and i suggest u to give more questions like this…
Shiva,
Thanks for the kudos
. An advanced interest post is definitely called for in the not too distant future.
Chris,
Can you explain the solution of Q2.
The question is basically saying that John earns $15 per month (on top of his 100). Thus it will take him 6.67 months to earn 100. Since he start investing at the beginning of January, he will earn 100 by the end of July.
Hope that helps
Wait, are you saying that when it says “monthly,” we still assume his account balance increases daily/hourly/etc? I understand that it’s 6.67 months, so technically it’s the end of July. But isn’t that assuming that the bank deposits his interest earnings every day or every hour, as opposed to the beginning of each month?
Thanks.
I had the same doubt.
As the account yields 15% interest monthly, shouldn’t the interest be reflected when a new month starts?
Hi Manan,
I responded to Zuhaib’s comment. Again, sorry for any confusion
.
Hmm, that is a good point. I was assuming that it increases every minute, but technically ‘monthly’ would mean only at the beginning of each month. So not the best question – my assumption would be far more valid if the question dealt with a constant growth rate, such as a population of bacteria.
Sorry for any confusion
.
Hi Chris,
So if we say that interest is added at the beginning of the month then the answer would be August, right? As he still has $190 at the beginning of July.
Also, this blog seems to have a few typos.
1. Q2 first it’s John then you say Mike!
Intro to compound interest: you state, after 10 yrs, mike will have 260, which is 60 more than mike
Wouldn’t that be bob has 260, which is 60 more than mike.
Thanks.
Btw, thanks for these blogs and comments. they’re very helpful!
Oh wow, you’re right! That is very confusing
. Note to self: do not use really generic names 
.
Thanks for catching that Shamila!
Chris:
Do you mind showing the steps you used to solve it? Thanks
Sure, I saw that the difference between ’06 and ’08 was $20. Thus each year is a $10 increase since are dealing with simple interest. If the accounted started in 01′ that means in 5 years (from ’01 to ’06), the account went up $50 (ten each year). So in 2001 account was $200 = x. If account increases $10 that is 5% of 200. So y =5. And x + y = 205.
Hi Chris,
Thank you for the explanation. How come y isn’t equal to 0.05? I thought the 5% would have to be added in decimal form, with x + y equaling 200.05.
Thanks!
Hi Helena,
That’s a tricky one! See the variable is presented as “x percent”. In this case, the number for x is simply 5, as in 5 percent. As an actual number, 5% is represented as .05, but if ‘x’ were to equal .05, we would have .05 percent, which is .0005.
Hope that clears things up
!
Hi Chris:
How did you come out with option E (210) on question 3?
Oops, that should be (D) 205
x = 200 and y = 5
Thanks for noticing that
.
Hey Chris,
Is it the word ‘ compounded ‘ that decides.the fate of the question or some other words are also included in the.pool..?
For compounded interest questions, ‘compounded’ determines the fate of the question.