Unlike Problem Solving, Data Sufficiency is a question-type unique to the GMAT. Data Sufficiency is part of the Data Insights section on the GMAT.
GMAT Data Sufficiency Practice Questions
1. Maggie is 15 years older than Bobby. How old is Bobby?
Statement #1: In 3 years, Maggie’s age will be 50% larger than Bobby’s age.
Statement #2: Years ago, when Maggie was 25 years old, Bobby was 10 years old.
2. By abc we denote a three digit number with digits a, b, and c. Is abc divisible by 3?
Statement #1: The product of (a) times (b) is a number divisible by 3
Statement #2: c = 3
3. The ratio of underclassmen to upperclassmen in a particular school is 4:5. How many underclassmen are there?
Statement #1: If the number of upperclassmen increased by 20%, then underclassmen would constitute 40% of this larger student body.
Statement #2: If 10 more underclassmen joined the school, the new ratio of underclassmen to upperclassmen would be 9:10.
4. An oddly shaped die has N sides, numbered from 1 to N, that are equally likely to appear on a throw. Let P be the probability that at least one “1” appears in two throws. Is P < (1/5)?
Statement #1: N is a prime number
Statement #2: N > 5
5. Set S consists of all the positive multiples of 5 that are less than K, and K is a positive integer not divisible by 5. The mean of Set S is not divisible by 5. Let N be the number of members of the set. N is not divisible by 5. What does N equal?
Statement #1: N < 52
Statement #2: K/5 > 48
6. The numbers D, N, and P are positive integers, such that D < N, and N is not a power of D. Is D a prime number?
Statement #1: N has exactly four factors, and D is a factor of N
Statement #2: D = (3^P) + 2
Answers and Solutions
1. Let M = Maggie’s age right now, and let B = Bobby’s age right now. The prompt gives us the equation M = B + 15.
Statement #1 gives us a second equation, (M + 3) = 1.5*(B + 3). Notice that I used a multiplier for the percent increase. With this equation and the prompt equation, we have two equations with two unknowns, so we can solve for the values of M & B. We don’t need to perform those calculations: it is enough to know that we could. This statement, alone and by itself, is sufficient.
Statement #2 is already obvious from the prompt. If Maggie is 15 years older than Bobby, then when Maggie was 25, Bobby would have had to have been 10. There’s no surprise there. We are given absolutely no indication when these people were these ages, so this doesn’t help us at all. This statement, alone and by itself, is not sufficient.
Answer = (A)
2. Remember, the divisibility rule: if the sum of all the digits in a large number is divisible by 3, then the number itself is divisible by three.
The problem with statement #1, for any given values of a & b that work, the one’s digit, c, could be anything. For example, a = 1, and b = 3 satisfy this condition, so that would be all the numbers in the 130’s: {130, 131, 13, 133, 134, 135, 136, 137, 138, 139}. Clearly, some of these are divisible by 3, namely {132, 135, 138} and the others aren’t. This statement allows for multiple answers, so this statement, alone and by itself, is not sufficient.
The problem with statement #2 is that we now know the one’s digit, but the other two digits could be anything. Think about the first few possible numbers of this form: {103, 113, 123, 133, 143, 153, 163, 173, 183, 193, 203}. Of those, only (123, 153, 183) are divisible by three, and the others aren’t. In fact, you would be expected to know this, but as it happens, {103, 163, 173, 193} are prime numbers, not divisible by anything! This statement also allows for multiple answers, so this statement, alone and by itself, is not sufficient.
Combined statements: now, we have to obey both constraints. One number that obeys both constraints is 133, which is not divisible by 3. Another number that obeys both constraints is 333, which is divisible by 3. Even with both statements in place, we can find numbers that produce either a “yes” or a “no” to the prompt. Even together, the statements are not sufficient.
Answer = (E)
3. We are given “ratio information” and we want actual numbers. To get counts, actual numbers of people, we need something besides more ratio information.
Statement #1 just gives us more “ratio information,” so we can’t solve for counts. This statement, alone and by itself, is not sufficient.
Statement #2 gives us some actual counts. Let N and P represent the current underclassmen and upperclassmen, respectively, in the school. We know N/P = 4/5 from the prompt. From this statement, we know (N + 10)/P = 9/10. Together, we have two equations for two unknowns, so we could solve for the values of N & P. This statement, alone and by itself, is sufficient.
Answer = (B)
4. First of all, if the N sides are equally likely, the probability of getting “1” on a single throw, or any particular side on a single throw, is 1/N. The probability of not getting “1” on a single throw, or not getting any particular side, is (1 – 1/N) = (N – 1)/N.
For relatively low values of N, then getting “1” is relatively more likely, and getting something else is relatively less likely. As N gets bigger, the probability of getting “1” on a single throw decreases, and the probability of getting something else increase.
What really makes the difference in this probability is the size of N. This is an at least probability, so we calculate the probability of getting something other than one on two consecutive throws, and then subtract this from 1.
Statement #1: this statement is not very helpful. If N = 2, then essentially, the “two-sided die” is a coin, and if H = 1, then the probability of not getting a “1” is (1/2). The probability of not getting a “1” on two consecutive throws is (1/4). That’s the probability of getting no “1” on two throws. We subtract this from one to get the probability of at least one “1”: P = (3/4), which greater than 1/5. Answer to the prompt = “no.”
But, suppose N is larger. For easy of calculation, I will pick N = 15, even though 15 is not prime. If N = 15 produces a probability less than 1/5, then so will any prime number greater than 15.
If N = 15, then the probability of not getting a “1” on a single throw is 14/15. The probability of not getting a “1” on two consecutive throws is this squared, 196/225. If this is more than 4/5, then subtracting it from one will be less than 1/5. Well, 225/5 = 45, and 45 times 4 is 180. Thus, (180/225) = (4/5), and (196/225) > (4/5). Subtracting this from one will produce a probability less than 1/5. Answer to the prompt = “yes.”
This statement is consistent with different answers to the prompt question, so it does not lead to a definitive answer. This statement, alone and by itself, is not sufficient.
Statement #2: We have already seen that N = 15, or any number larger than that, produces a “yes” answer to the prompt. Is it possible to produce a “no” answer to with a value of N greater than 5?
I will use N = 7. The probability of not getting a “1” on a single throw is 6/7. The probability of not getting a “1” on two consecutive throws is this squared, 36/49. If this is less than 4/5, then subtracting it from one will be more than 1/5.
Well, clearly, 36/45 = 4/5, and making the denominator larger makes a fraction smaller, so
4/5 = 36/45 > 36/49. So, this fraction is less than 4/5, so subtracting it from one will result in a probability that is greater than 1/5. This gives a “no” answer to the prompt.
This statement is consistent with different answers to the prompt question, so it does not lead to a definitive answer. This statement, alone and by itself, is not sufficient.
Combined statements: As we saw in the previous statements, the prime number N = 7 gives a “no” answer, and the non-prime N = 15 gives a “yes” answer, which implies that any prime number greater than 15 (such as 17, 19, 23, etc.) would also give a “yes” answer. Different answers are possible even with the constraints of both statements. Together, both statements are still not sufficient.
Answer = (E)
5. This is a tricky problem, because there are several constraints in the problem. first of all, the number of members is N, so the numbers in the set go from 5 to 5N. The integer K has the quality that 5N < K < (5N + 5), because K is bigger than the biggest member of the set, but 5N has to be the largest multiple of 5 less than K.
We know that the mean of the set is not divisible by 5, and this is important. For an evenly spaced set, the mean & median are identical. If there were an odd number of members, the mean & median would simply be the middle number on the list, and this of course would be some multiple of 5. The fact that mean & median is not divisible by 5 necessarily means that there must be an even number of members on the list. This way, the mean & median would be the average of the middle two numbers, which would be a non-integer, certainly not an integer divisible by 5. Therefore, N is an even number.
Finally, we are also told that N itself is not divisible by 5—an odd constraint that may be relevant.
Statement #1: Here, N could be any even number less than 52, as long as it’s not divisible by 5. It could be {48, 46, 44, 42, 38, ….} Multiple possibilities. This statement, alone and by itself, is not sufficient.
Statement #2: The statement tells us that K > 5*48, so it could be that N = 48, so that K would be between 5(48) and 5*(49). That’s a possibility, or N could be any larger even number that is not divisible by 5. N could be {48, 52, 54, 56, 68, 62, …} Again, multiple possibilities. This statement, alone and by itself, is not sufficient.
Combined statements: with both constraints, the only possible value if N = 48. The statements together are sufficient.
Answer = (C)
6. This is a tricky one.
Statement #1: two kinds of numbers have exactly four factors: (a) products of two distinct prime numbers, and (b) cubes of prime numbers.
The product of two distinct prime numbers S and T would have factors {1, S, T, ST}. For example, the factors of 10 are (1, 2, 5, 10), and the factors of 21 are {1, 3, 7, 21}.
The cube of a prime number S would have as factors 1, S, S squared, and S cubed. For example, 8 has factors {1, 2, 4, 8} and 27 has factors {1, 3, 9, 27}.
We know N is not a power of D, so the second case is excluded. N must be the product of two distinct prime numbers. We know D < N, so of the four factors, D can’t be the product of the two prime numbers. D could be either of the prime number factors, or D could be 1, which is not a prime number. Because D could either be a prime number or 1, we cannot give a definitive answer to the question. This statement, alone and by itself, is not sufficient.
Statement #2: this is tricky. The first few plug-ins seem to reveal a pattern.

Even if you sense a pattern, it’s important to remember that plugging in numbers alone is never enough to establish that a DS statement is sufficient. Here, if we persevered to one more plug-in, we would find the one that breaks the pattern.
![]()
That gives another answer to the prompt, so we know this statement is not sufficient.
To avoid a lot of plugging in, it’s also very good to know that in mathematics, prime numbers are notorious for not following any easy pattern. It is impossible to produce an algebraic formula that will always produce prime numbers. In fact, this is more than you need to know, but the hardest unsolved question in higher mathematics, the Riemann Hypothesis, concerns the pattern of prime numbers; mathematicians have been working on this since 1859, and no one has proven it yet. Suffice to say that no one-line algebraic formula is going to unlock the mystery of prime numbers!
Combined statements: according to the information in statement #1, either D = 1 or D is a prime number. Well, statement #2 excludes the possibility that D = 1, because that number cannot be written as two more than a power of 3. Therefore, D must be a prime number. We have a definitive answer to the prompt question. Combined, the statements are sufficient.
Answer = (C)
DS Probability Questions
1. A class contains boys and girls. What is the probability of selecting a boy from a class?
Statement #1: there are 35 students in the class
Statement #2: the ratio of boys to girls is 3:4
2. Bert has $1.37 of loose change in his pocket —- pennies ($0.01), nickels ($0.05), dimes ($0.10), and quarters ($0.25). He reaches into his pocket and pulls out one coin at random. What is the probability that the coin is a nickel?
Statement #1: There are exactly seven pennies in his pocket
Statement #2: There are exactly three quarters in his pocket
Answers:
1. Statement #1: from this, we know there are 15 employees selected. We don’t know the value of M, which is clearly greater than or equal to 15. If M is very large, it may be highly unlikely that either Andrew or Georgia is seated. If M is closer to 15, then that would change the probability. Without knowing the value of M, we can’t complete the calculation. This statement, alone and by itself, is insufficient.
Statement #2: Ignore the information in the first statement. If M = N, then all employees, everyone in the pool of selection, takes a seat. It is simply a matter of seating a group of M employees randomly in M seats.
Think about this. For every seating arrangement with Andrew to the right of Georgia, there will be exactly one seating arrangement, the mirror image, that has Andrew to the left of Georgia. Since there’s a one-to-one correspondence between these two, there must be just as many arrangements with Andrew on one side of Georgia as on the other side. Both are equally likely, so the probability must be 1/2.
This information was enough to calculate a numerical answer to the prompt question. This statement, alone and by itself, is sufficient.
First not sufficient, second sufficient. Answer = B.
2. A reminder for non-American students — $1.00 = 100¢. Thus
penny = $0.01 = 1¢
nickel = $0.05 = 5¢
dime = $0.10 = 10¢
quarter = $0.25 = 25¢
Statement #1: Bert has seven pennies, amounting to 7¢. The other coins total $1.30. This could be all nickels — 26 nickels — so that of the 7 + 26 = 33 coins in the pocket, 26 are nickel, and the probability of picking a nickel would be 26/33. Or, that $1.30 could be 4 quarters and 3 dimes, so that there were no nickels, and the probability of picking a nickel would be zero! Different possible choices lead to different answer to the prompt question, so this statement, alone and by itself, is insufficient.
Statement #2: Bert has three quarters, amounting to 75¢. The other coins total 62¢ — this could be two pennies and twelve nickels, that of the 3 + 2 + 12 = 17 coins in the pocket, 12 are nickels, and the probability is 12/17. Or, that 62¢ could be entirely in pennies, without any nickels or dimes at all: then the probability of picking a nickel would be zero. Different possible choices lead to different answer to the prompt question, so this statement, alone and by itself, is insufficient.
Combined statements: Now, we know Bert has seven pennies and three quarters, and these ten coins together account for 82¢. The remaining 55¢ must be composed of dimes and nickels. There could be eleven nickels and no dimes, so that of the 10 + 11 = 21 coins in the pocket, 11 are nickels, and P = 11/21. OR, there could be five dimes and one nickel in the pocket, so of the 10 + 5 + 1 = 16 coins in the pocket, only one is a nickel, and P = 1/16. Different possible choices lead to different answer to the prompt question, so both statements combined are insufficient.
Nothing is sufficient. Answer = E
Try This Tricky Data Sufficiency Question!
On each lab that René completed he received either 100 points or 85 points. On how many labs did he score 100 points?
-
(1) René’s scores for his completed labs totaled 1140 points.
(2) René completed a total of twelve labs.
(A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
(B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
(C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(D) EACH statement ALONE is sufficient.
(E) Statements (1) and (2) TOGETHER are NOT sufficient
Answer and Explanation
This problem yields a system of linear equations.
Let the number of labs on which René earned a score of 100 points=x.
The total score for these labs=100x.
Let the number of labs on which René earned a score of 85 points=y.
The total score for these labs=85y.
The total score for all labs=100x+85y.
The question asks us to solve for x.
Statement (1) can be rewritten as 100x+85y=1140.
Statement (2) can be rewritten as x+y=12.
When a DS story problem yields a system of distinct linear equations but implicitly requires that solutions be integers, the smart thing to do is to test values. Generally the numbers involved won’t be very large, so the arithmetic won’t be too daunting.
Statement (1): First, stipulate an integer value for y, then calculate 85y, then subtract that product from 1140. If the difference left isn’t a multiple of 100, don’t consider it further:
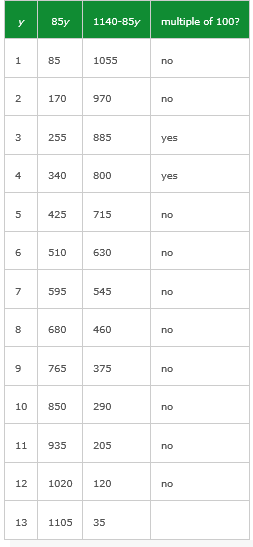
Since only one integer value for y yields an integer value for x, and since both x and y must be integers, Statement (1) is sufficient. Eliminate B, C, and E.
Statement (2): Any pair of integers that sum to 12 is a possible pair of values for x and y, so Statement (2) is not sufficient. Eliminate D. The correct answer is A.






Leave a Reply