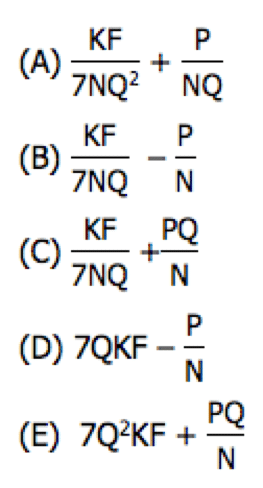In the course of studying for the GMAT, naturally you do GMAT practice problems. When you do the problems, then grade them, how do you learn from them? What are the ways you can maximize your learning from the practice problems you do?
First of all, perhaps to belabor the obvious — you need more than “answers” —- you need full solutions, full explanations. If you are using a practice questions source that only gives you answers and no explanations or solutions, that is probably not going to help you much. Most good sources have a written explanation. Magoosh, in addition to text explanations, also has a video explanation for each and every practice question. Given resources such as this, how do you learn?
Reading the solutions
Many students do the problems, and then read the solutions for what they got wrong. Let’s think about this. Reading the solution and thinking, “Yes, I see now, that makes sense” — how useful is this? It’s a little like wanting to know how to hit a golf ball hundreds of yards, then watching some pro on TV do it in a tournament, saying, “OK, I see how he does it,” and thinking that one is thereby an expert. Similarly, watching someone sketch a face, watching someone ride a unicycle, or watching someone perform the Beethoven Violin Concerto. Watching something done well does not automatically translate into being able to do it one’s self. Passively reading the solutions to problems may help if you understood everything else and just needed a reminder or clarification about one particular issue, but if you want to make substantial gains in your performance, you will probably have to strive to get significantly more from your post-problem analysis.
Getting more
One question to consider: should you look at solutions only for questions you got wrong? If you are very weak in a particular area, you need at least to explore the question: are you getting questions correct for the right reasons? Until you have enough confidence in an area that you can say, with reasonable certainty, that the questions you are getting correct, you have gotten correct for the right reasons — until you know that, you need to read all solutions, even the questions you got right, to verify that what you thought was right really is right.
OK, when you read the solutions, for what should you be looking? Any solution is demonstrates a process of analysis, and in addition to the individual steps or points, you need to think about how this process is organized. Why did the solution start that way? What about the problem made the author of the solution start that way? What choices did the author make in the process of working through the solution? How the facts are organized is more important than any individual fact.
In any given math problem, there may be 20 or 30 different individual math facts you need to know to get to the answer, if you know, say, 28 or 29 out of the 30, you will not get the answer. Pay attention to the math facts that are obvious once the solution states them — will they be obvious to you when you work through a problem on your own? Think about math at the level of strategy — not just what step the solution took at each point, but why it took that step rather than any other possible step. At any point in a math problem, there are often multiple mathematically legal steps one could take, but only one or two that would be the most strategic to take. Understanding math well means thinking past the individual math factoids to the strategic architecture of the solution.
The ideal
The mark of a truly exceptional student is: never making the same mistake twice. This is a lofty ideal, hard to live by. If, in striving for this ideal, you are only, say, 50% successful, you will still be well on your way to excellence.
Challenge yourself: when you get a question incorrect, what do you have to do to guarantee that you will not make that mistake again? This may involve actually writing out an explanation of what you got wrong, the nature of the mistake, and the thing you will not repeat the next time in that kind of problem. Forcing yourself to articulate the solution in words creates important connections in the brain. Obviously, this takes considerably more time and energy than just a casual perusal of the solution, but think of it as a wise investment: learning with that level of depth and rigor will have broad payoffs, especially when you practice it consistently over time.
Think in terms of the depth vs. breadth trade-off. Many GMAT students are drawn to breadth, wanting to practice hundreds or thousands of practice problems. That’s great, but if pursuing that much breadth means not gaining a deep understanding, it’s not necessarily a recipe for success. Success usually requires a combination of breadth and depth. The techniques I discuss here for “not making the same mistake twice” represent an emphasis on depth that could well complement an otherwise broad approach.
Summary
Here are a couple challenging practice problems:
1) a DS problem: http://gmat.magoosh.com/questions/943
2) a SC question: http://gmat.magoosh.com/questions/3218
You can use these questions for some “depth” practice! If you would like to respond to what I have said here, or if you have a question, please let us know in the comments section below.