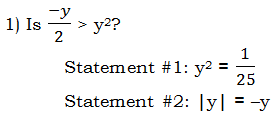First of all, for warm-up, a practice Data Sufficiency question.
The symbol
What does this symbol mean in math?
Technically, this symbol, typographically a dash, has three different meanings in mathematics, viz.:
a) a subtraction sign
b) a negative sign
c) an opposite sign
The subtraction sign
When the dash appears between two terms — between two numbers (5 – 3), between two variables (x – y), between a number and a variable (x – 2), etc. — then it indicates the operation of subtraction. This is, undoubtedly, the very first meaning folks associate with the dash, because folks learned this way back in grammar school math. Furthermore, as soon as kids understand money and spending money, essentially they understand something about subtraction, so rare is the kid who doesn’t get subtraction early on.
The negative sign
When the dash appears in front of a stand-alone number (–5, –2.7, 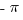 , etc.), then it is a negative sign, denoting that the number in question is less than zero and to the left of zero on a standard number line. Folks tend to learn this idea relatively early on as well. Moreover, it’s easy to see how this meaning “blurs” into the subtraction-sign meaning, because after all, 8 + (–2) is just another way of saying 8 – 2. Both have a kind of “minus-making” meaning to them.
, etc.), then it is a negative sign, denoting that the number in question is less than zero and to the left of zero on a standard number line. Folks tend to learn this idea relatively early on as well. Moreover, it’s easy to see how this meaning “blurs” into the subtraction-sign meaning, because after all, 8 + (–2) is just another way of saying 8 – 2. Both have a kind of “minus-making” meaning to them.
The opposite sign
This is the one that can through folks into a tizzy. When you put the dash not in front of a stand-alone number but rather a stand-alone variable, then it is NOT a negative sign anymore. Rather, it is an opposite sign, which changes the sign of the variable to the opposite of whatever it was originally. If y is a positive, then –y is negative. BUT, if we know y is negative, then we know –y is positive.
Right there, that is precisely what wigs people out! Since before puberty, they were accustomed the dash having a universal “negatizing” effect, and yet, in this strange instance, when y is already negative, the dash in front of –y actually makes it positive. To some folks, this seems an unholy violation of everything they have ever learned about the sign! Technically, folks learn about the opposite sign somewhere in algebra, but it is seldom explained well there, setting folks up for this massive confusion when they encounter the opposite sign on, for example, the GMAT Quantitative section.
For example, the algebraic statement:
|y| = –y
is a sophisticated way of indicating that y ≤ 0. Conceivably, the GMAT could give you the former and expect you to deduce the latter.
Practice
It may be that the foregoing discussion gave you some insight into the practice question at the top of this pages. Take another look at that before reading the solution below. Also, here’s a free practice question with some positive/negative variable issues.
2) http://gmat.magoosh.com/questions/301
Practice Problem Solution
1) This is a difficult DS question. First of all, some folks might mistakenly think the prompt is already decided as it is written. After all, we know that the right side of the inequality,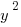 , is always positive. Some folks may mistakenly think that the left side of the inequality is always negative, but that would entail reading the dash incorrectly as a negative sign, rather than correctly as an opposite sign.
, is always positive. Some folks may mistakenly think that the left side of the inequality is always negative, but that would entail reading the dash incorrectly as a negative sign, rather than correctly as an opposite sign.
Statement #1 implies that y = ±1/5. (How do you know you have to take both the positive and negative square roots? See this GRE post.) Those two values imply different conclusions to the prompt. If y = +1/5, then –y/2 = –1/10, which is clearly less than 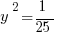 . But, if y = –1/5, then –y/2 = +1/10, which happens to be greater than
. But, if y = –1/5, then –y/2 = +1/10, which happens to be greater than 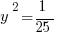 . The two different possible values imply different conclusions, which means no definitive answer to the prompt is possible. This statement, by itself, is insufficient.
. The two different possible values imply different conclusions, which means no definitive answer to the prompt is possible. This statement, by itself, is insufficient.
Statement #2 is a fancy way of saying that y ≤ 0. If y = –5, then the inequality is false, but if y = –1/100, then –y/2 = +1/200, which is greater than 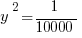 , and the inequality is true. Two different possible values imply different conclusions, which means no definitive answer to the prompt is possible. This statement, by itself, is insufficient.
, and the inequality is true. Two different possible values imply different conclusions, which means no definitive answer to the prompt is possible. This statement, by itself, is insufficient.
Statement combined: when we combine the restraints of both statements, we know that y can only have one value: y must equal –1/5, and this, by itself leads to a definite answer to the prompt. Thus, the combined statements are sufficient.
Answer = C.