GRE Math: Ratios

February 17, 2012

Ratios are one of those concepts that can pop up in just about any GRE problem. You could have the ratio between two angles that form from intersecting lines. You could have the ratio of rates a person drove at. With such a broad application, ratios are one of the concepts it is imperative you learn now.

To see how ratios work – and to see the type of problems the GRE will devise to try to trick you – let’s try a few simple problems first and then some challenging ones.

GRE Ratio Practice Problem

1. Tom is selling apples and oranges. The ratio of apples to oranges in his cart is 3:2. If he has 12 oranges, how many apples does he have?

(A) 2 (B) 3 (C) 8 (D) 18 (E) 30

Solution:

A ratio is basically a fraction that has been reduced as much as possible. In this problem the ratio 3:2, can be represented as 3/2. One way to solve this problem is to set up a simple equation:

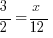
Notice I placed the 12, the number of oranges, in the denominator. We have to make sure that the number 12 corresponds to 2, the oranges in the ratio. Solving for x, we get 18 (D).

An even quicker way is to notice that we have (x6) the oranges (from 2 we go to 12) so we just have to (x6) the apples in the ratio: 3 x 6 =18.

Now’s let’s try the same question but with a spin:

2. Tom is selling apples and oranges. The ratio of apples to oranges in his cart is 3:2. If he has a total of 30 fruits, how many apples does he have?

(A) 2 (B) 3 (C) 12 (D) 18 (E) 30

Solution:

This question, while essentially the same, is the one that gives students a lot more trouble. The problem is combining two concepts: ratio and total. To do so simply add the ratios. We have 3:2 so the total is 5.

One way to solve the problem is to set up the table. Tables are great both from a teacher’s and beginner’s standpoint. In this case, I get to show you a nice, tidy way of solving the problem and you have an easy way both to conceptualize and solve the problem.

However, once you become used to tables, in the interest of time, learn to solve a ratio without one (I’ll show you how to do so in a second!).

	Apples	Oranges	Total
Ratio	3	2	5
M(x)
Actual	?	?	30

What do we multiply the total ratio by to get the actual total? (x6).

So in the middle row in the total column we can place a 6.

	Apples	Oranges	Total
Ratio	3	2	5
M(x)	6	6	6
Actual	18	12	30

Notice the (M)x, which stands for multiply (you can dispense with the M, I just didn’t want anyone thinking there is this random variable x floating around).

Now we multiply the apples and oranges by 6 to get 18 and 12, respectively.

Remember the faster way I mentioned?

Add the ratio
Figure out the x6
Multiply 3 x 6

18 (D). Also remember not to mix up apples and oranges. A classic trick on the GRE is they reverse the order.

Practice Questions

Okay, you’ve got the hang of ratios. Now you want something a little more challenging. Voila – it’s the ratio challenge workout.

The problems below appear superficially similar. Yet, the math behind each is different. Nonetheless, each of them deals with ratios, and will put your ability to the test. The problems tend to get progressively harder. So if you struggled at the end, don’t despair. As long as you can nail the first three, you’re doing pretty well on ratios.

Good luck!

1. A jewel necklace contains only emeralds, rubies, and diamonds. If the ratio of emeralds to diamonds is 2:7 and the ratio of diamonds to rubies is 3:2, then which of the following could not be the number of jewels on the necklace?

(A) 41

(B) 81

(D) 123

(E) 205

2. A tiara is studded with a mixture of gems. The ratio of sapphires to emeralds is 3:1. If 6 emeralds are added, the tiara will contain an equal number of sapphires and emeralds. How many emeralds must be added to the original tiara so that the ratio between emeralds and sapphires is 3:1?

(A) 9

(B) 12

(D) 24

(E) 27

3. An imperial scepter is mounted with diamonds, rubies, emeralds, and sapphires in the ratio of w : x : y : z. If w, x, y, and z are distinct single digit primes, then how many gems could be on the imperial scepter if it only contains the gems listed above?

(A) 19

(B) 58

(D) 97

(E) Cannot be determined from the information provided above.

4. (Okay – enough with the jewels!) Marty has a coin collection, which consists of only New World and Old World coins, in a ratio of 3:1. Marty’s friend Kyle swaps 28 of his Old World Coins for 28 of Martin’s New World coins. If Marty now has as many Old World coins as he does New World coins, how many coins did Marty originally have in his collection?

(A) 28

(B) 84

(D) 130

(E) 390

5. (Okay, back to jewel necklaces). Marty has a necklace that contains a total of 36 rhinestones, zirconium, and obsidian “gems.” If the ratio of obsidian to zirconium is 2:5, then which of the following could not be the number of rhinestones in Marty’s necklace?

(A) 8
(B) 12
(C) 15
(D) 22
(E) 29

Answers:

1. B

2. D

3. C

4. C

5. B

Special Note:

To find out where ratios sit in the “big picture” of GRE Quant, and what other Quant concepts you should study, check out our post entitled:

What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency

Author

Chris Lele

Chris Lele is the Principal Curriculum Manager (and vocabulary wizard) at Magoosh. Chris graduated from UCLA with a BA in Psychology and has 20 years of experience in the test prep industry. He’s been quoted as a subject expert in many publications, including US News, GMAC, and Business Because. In his time at Magoosh, Chris has taught countless students how to tackle the GRE, GMAT, SAT, ACT, MCAT (CARS), and LSAT exams with confidence. Some of his students have even gone on to get near-perfect scores. You can find Chris on YouTube, LinkedIn, Twitter and Facebook!

View all posts

Share5

Pin1

Comments

48 responses to “GRE Math: Ratios”

rutuja

April 20, 2023

can you explain question 5?

Reply
1. Magoosh Test Prep Expert
  
  April 21, 2023
  
  Hi Rutuja,
  
  Thanks for asking! The keys here are that the ratio of obsidian (“o”) to zirconium (“z”) must be 2:5, the total gemstones must add up to 36, and there must be a whole number of gemstones only. We can’t have a fraction of a gemstone.
  
  So there are only the following possibilities:
  
  | o | z | r | total |
  |—|—-|:–:|–|
  | 2 | 5 | 29 | 36 |
  | 4 | 10 | 22 | 36 |
  | 6 | 15 | 15 | 36 |
  | 8 | 20 | 8 | 36 |
  
  So r = 12 is not a possibility.
  
  Also notice that, since the ratio of o:z = 2:5, o + z is always a multiple of 2 + 5 = 7…2 + 5, 4 + 10, 6 + 15…etc.
  
  So the fastest way to do this is to take 36 and keep subtracting 7:
  
  36 – 7 = 29
  – 7 = 22
  – 7 = 15
  – 7 = 8
  
  Happy studying! 😀
  
  Reply
Mohamed

April 10, 2022

thanks for the explanation. I read that you are explaining the answers in videos but I could not locate them. Could you please provide the link

Reply
1. Magoosh Test Prep Expert
  
  April 22, 2022
  
  Hi Mohamed,
  
  Thanks for asking! Unfortunately, the videos are no longer available. I’m sorry for any inconvenience this may cause you, but I do hope the written explanations included in the article help!
  
  Happy studying! 😀
  
  Reply
Amna

December 7, 2019

For Question 1, the only possible answer I get is 41. I think all except 41 are impossible. Can you please elaborate a bit. ?

Reply
1. Magoosh Test Prep Expert
  
  December 7, 2019
  
  Hi Amna! By converting the ratios so we have emeralds:diamonds 6:21 and diamonds:rubies 21:14, we find that emeralds:rubies:diamonds is the equivalent of 6:14:21. That means that the minimum total number of jewels is 41. This is the standard approach to combining two ratios. We have to find a common number that allows us to combine them. We can’t combine 2:7 and 3:2, but we can convert them to 6:21 and 21:14 and use that common number to combine. 41 is the minimum number of jewels because we add up the numbers in the ratio, but this isn’t the only possible total. It also could be 41*2 = 82, 41*3 = 123, 41*4 = 164, 41*5 = 205, etc. The only number that can’t be the number of jewels is 81 because that’s not an integer multiple of the minimum total. To get 81, we’d need a piece of a jewels, so choice (B) 81 is the only answer choice that couldn’t be the total number of jewels. 41 is a great start because it’s the minimum, but we have to look at the multiples as well.
  
  Reply
Rahul

August 6, 2019

Hi chris in questioin 5 why can’t i add the ratio of obsidian to zirconium and have a ratio of 7x : ?? = 36 to simplify the calculation.
Thanks

Reply
1. David Recine
  
  August 13, 2019
  
  Actually, you can, Rahul. The main reason that wasn’t mentioned in the explanation, is that adding 5+2 and simplifying to 7 is a very sophisticated “number sense” short cut that not every student would think of naturally. But it is a really great approach that shows some nice math skills on your part!
  
  Reply
Abhishek

September 10, 2018

Hi chris
Can you explain me question no 5 solution?
I am vague about it.

Reply
1. Magoosh Test Prep Expert
  
  September 16, 2018
  
  Hi Abhishek,
  
  Can you please provide some more detail about what you found challenging about this question? What part of the explanation didn’t make sense to you? Simply re-stating the explanation probably won’t help you much unless you provide some more detail about your own thought process.
  
  Reply
Ali

March 2, 2017

Hi Chris,
Thanks for the detailed explanations. I am stuck on #4 & still getting 224 instead of 112..

Reply
1. Magoosh Test Prep Expert
  
  March 3, 2017
  
  Hi Ali,
  
  So, we are told that Marty has “New World and Old World coins in a ratio of 3:1”. So, if he has x Old World coins, he has 3x New World coins. His friend Kyle takes 28 of Martin’s New World coins, and gives Marty 28 Old World coins. This means Marty’s New World coins become (3x – 28). Marty’s Old World coins become (x + 28).
  
  With this change, Marty’s New World and Old World coins equal:
  
  New World = Old World
  3x – 28 = x + 28
  
  So, now it’s a matter of calculation:
  
  3x – 28 = x + 28 [Add “28” to both sides]
  3x = x + 56 [Subtract “x” from both sides]
  2x = 56 [Divide “2” from both sides]
  x = 28
  
  So, the question asks how many coins did Marty have originally? He had x Old World coins and 3x New World coins for a total of 4x coins.
  
  = 4x [Plug in x = 28]
  = 4(28) [Multiply]
  = 112
  
  I hope this helps! 😀
  
  Reply
  1. Rishiraj
    
    October 20, 2017
    
    How did you know that we had to assume the old world coins as ‘x’ and not the new world coins ? What happens if we do it otherwise ?
    
    Reply
    1. Magoosh Test Prep Expert
      
      October 21, 2017
      
      Hi Rishiraj,
      
      For ratio questions, we must create our own ratios based on the information in the question, but you can definitely choose how you decide to define different terms. We are given the information: Marty has a coin collection, which consists of only New World and Old World coins, in a ratio of 3:1. This means that Marty has 3 New World Coins for every 1 Old World Coin. It also means that Marty has 1/3 of an Old World Coin for every New World Coin. If you want to define x as New World Coins, you would have the following ratio:
      New World Coins: Old World Coins
      x:1/3x
      This is equivalent to the ratio we used in this question and you will get the same answer if you solve the question with this ratio, but you’ll notice that this will be more difficult to deal with. When defining your terms, we must be aware of how our definitions impact the question. In this case, it’s must easier to deal with an integer than a fraction, which is why we defined x as old world coins in this question. Does that make sense?
      
      Reply
Nafiz

February 19, 2017

Hi Chris
i couldn’t solve the question 2 in practice section …. :/
plz help

Reply
1. Magoosh Test Prep Expert
  
  February 21, 2017
  
  Hi Nafiz!
  
  Happy to help 🙂
  
  In this problem, we’re told that the original ratio of sapphires to emeralds on the tiara is 3:1 or for every 3 sapphires there is 1 emerald. This doesn’t mean that there are only 3 sapphires and 1 emerald but rather that the
  
  number of sapphires = 3n
  number of emeralds = n
  
  where n is the scale factor or number we can multiply the ratio by to find the actual number of each gem.
  
  So, there are n emeralds on the tiara. We’re told that if we were to add 6 emeralds, the number of sapphires and emeralds would be equal:
  
  n + 6 = 3n
  
  And we’re asked to determine how many emeralds must be added so that
  
  emeralds : sapphires = 3 : 1
  
  First, let’s figure out n, the scale factor, using the equation I wrote above:
  
  n + 6 = 3n
  6 = 2n
  3 = n
  
  So, n = 3 and
  
  # emeralds = n = 3
  # sapphires = 3n = 3*3 = 9
  
  Now, we need to add a certain number of emeralds so that emeralds/sapphires = 3/1: (3 + x)/9 = 3/1, where x is the number of emeralds we’re adding. So, let’s solve for x!
  
  (3 + x)/9 = 3/1
  (3 + x) = 3*9
  3 + x = 27
  x = 24
  
  This is answer choice (D), the correct answer 😀
  
  I hope this clears up your doubts about this problem. If not, please let us know 🙂
  
  Reply
  1. Nafiz
    
    February 21, 2017
    
    Wow …
    um did up to the number of the individual gems but after that i just stucked.
    Thank u so much for ur help … 😀
    
    Reply
Luis

January 24, 2017

i got them right when i did them, but the worrisome part is that i took too long. That’s the big problem. I’m looking for a way to “mechanize” the process. What do you guys recommend?

Reply
1. Magoosh Test Prep Expert
  
  January 25, 2017
  
  Hi Luis,
  
  If you’ve identified Ratios as a subject that you need to improve in your speed, I would highly recommend taking more time to prepare for this section. Given that you’re able to get the answers correct when the clock is not an issue, I would slowly provide yourself a time restriction to practice on speed. Start small. Then, slowly build yourself up to 1 min 45 seconds. It’s important to maintain accuracy as you improve speed.
  
  Unfortunately, there is no easy way to “mechanize” the way of solving all ratio problems. Our explanations are a good source to use in understanding efficient approaches to solve these problem. With practice and exposure to more problems, you can quickly identify how to approach a problem to improve your speed. I would definitely recommend continuing to do more Ratio problems to practice and gauge your progress! Good luck!
  
  Reply
ananthu

December 8, 2016

Hi,

I was able to crack every single question but I took some time (around 2min). Is there any way I could improve my speed on such questions and questions in Quant in general? any shortcut methods to save time? Time is the only thing which I find hard to deal with and not the questions themselves..

Regards,

Reply
1. Magoosh Test Prep Expert
  
  December 9, 2016
  
  Hi Ananthu,
  
  Great job solving all the problems correctly! Yes, pacing and speed is definitely a struggle that a number of students face. For every problem, please note that there are multiple approaches to solve the problem. And, as you’ve stated, some of these approaches are much more efficient. One of the best suggestions I could provide in learning multiple approaches will be to ALWAYS review the explanations regardless of whether you got the problem correct or incorrect. Even for those problems you get correct, the explanation may approach the problem in a different way that you may find more efficient. One of the best ways to learn multiple approaches is through these explanations. In addition, I would definitely recommend utilizing test prep resources, such as Magoosh, as they present various approaches through the lessons. If you are not already a Magoosh premium student, I would recommend trying out our 1-Week Free Trial.
  
  Finally, speed comes with practice. As you continue studying, try different practice sessions in which you test and limit your timing. You’ll find that you tend to solve certain topics or problem types more slowly than others. Understanding this will be good for your practice, as well as building a strategy for your actual test day. Good luck! 😀
  
  Reply
Daniel

October 27, 2016

Hello Chris,

Firstly, thanks for your help on all these topics.

Surprisingly, I found the the first 2 Q’s a lil tough, but cracked the other 3 in no time.

Any ideas?

Reply
1. Magoosh Test Prep Expert
  
  October 27, 2016
  
  Hi Daniel,
  
  Did you watch the explanations, and do the first two questions now make sense? If not, do you have any specific questions regarding to what you’re struggling with, so I can provide a more targeted response to you. Regardless, remember that practice makes perfect!
  
  Reply
Kishore A

May 22, 2016

Got all the problems right! Took some time though:-(

Reply
Monkey D Luffy

March 2, 2016

could you help me out with question no 3 im stuck

Reply
1. Magoosh Test Prep Expert
  
  March 4, 2016
  
  Hi there 🙂
  
  In this problem, we’re told that w, x, y, and z are distinct single digit primes. With that information, we can list the values for these variables:
  
  2, 3, 5, 7.
  
  It doesn’t matter which variable goes with which prime number. The important aspect of having four unique variables is that each one has a different value. So, once we have the four values, we know that the ratio of the gems is
  
  2:3:5:7
  
  If there were only 2, 3, 5, and 7 of the different gems, then the total would be the sum of this ratio:
  
  2+3+5+7 = 17
  
  However, 17 is not an answer choice. This indicates that the ratio 2:3:5:7 is a simplified ratio and that there is a common factor, n, that we must multiply the ratio by to get the actual number of gems.
  
  2n:3n:5n:7n
  
  If we were to find the sum of the number of gems using the ratio above, then, we would have
  
  2n + 3n + 5n + 7n = 17n,
  
  which shows us that the actual number of gems must be a multiple of 17. Out of the possible answer choices, only C (17*5 = 85) is a multiple of 17. So the correct answer is C 🙂
  
  I hope this helps!
  
  Reply
  1. Laiuren
    
    May 12, 2018
    
    But if the ratio becomes 2n:3n:5n:7n=17n, then w,x,y,z are no longer single digit prime numbers. For example n=5; 10:15:25:35 Doesn’t this conflict with the parameters of the question?
    
    Reply
    1. Magoosh Test Prep Expert
      
      May 14, 2018
      
      It doesn’t actually conflict with the parameters of the question, because w, x, y, and z don’t represent the actual number of each jewel. Instead, they represent the *ratios* of each jewel to the other. Ratio numbers of single digit primes mean that there could be a single digit prime value for each variable, OR that each variable is a *multiple* of a single digit prime. And in the case of your example– 10:15:25:35– each variable is a multiple of the single digit primes, in line with the constraints of the problem.
      
      Reply
Julio

July 16, 2015

Hi Chris,

In problem 5 I’ve been trying to figure out how to place the number 22 (answer D) in the ratios as to discard it, but I just can’t. How is it 22 is not an answer like 12?

Reply
1. Anonymous
  
  August 11, 2015
  
  You can have 4 obsidian, 10 zirconium, and 22 rhinestones. Thus, a ratio of 2:5:11.
  
  Reply
Nika

September 28, 2013

OMG I just got it!! They switched Emeralds and sapphires! ugh

Reply
1. Chris Lele
  
  October 1, 2013
  
  Great! Glad to hear that :). Sometimes, it’s just seeing that one little thing that opens up the entire problem.
  
  Reply
Nika

September 28, 2013

I think I’m getting confused on question # 2 because of the way I’m reading it. I think misinterpretation on the math will hurt me more than math itself. Can you help? The passage says:

“A tiara is studded with a mixture of gems. The ratio of sapphires to emeralds is 3:1. If 6 emeralds are added, the tiara will contain an equal number of sapphires and emeralds. How many emeralds must be added to the original tiara so that the ratio between emeralds and sapphires is 3:1?”

I’m reading it as you have a tiara where the ratio of sapphires to emeralds is 3:1. Good so far. But then 6 Emeralds are added to this tiara throwing the ratio off making it 1:1. We should have more sapphires than Emeralds to stick with the original ratio of 3:1. Now here is where I get stuck. If you added 6 emeralds and it was already to much. Making the ration 3:3 or 1:1 why would you add more? I understand the math works and it comes out to 24. But when I read the question it makes no since to me. If adding 6 emeralds makes the the ratio go up why would we add 24? That’s where I’m confused. Not so much the math. But I can’t tie it back to the question to make real world sense. There must be something I’m not reading right.

Reply
Chris

September 16, 2013

Chris thank you for all your explanation but I am stuck in number 1# do you have anything else to support it that will help me understand better. If I have to elements to compare I am fine and I do well but having a third element become difficult to me.

Thank you

Reply
1. Chris Lele
  
  September 16, 2013
  
  Yes, the three ratios are difficult because there is a “mismatch”. You have to think of the three ratios as a fraction in which you have to find a common denominator. So with question 1):
  
  Emeralds : Diamonds is 2 : 7
  
  Diamonds : Rubies 3 : 2.
  
  Next, look for what the two pairs have in common: Diamonds. Notice that in the first pair the number 7 corresponds to diamonds, and in the second set 3 corresponds to diamonds. 3 and 7 are totally different numbers. How do we make them similar? By finding their lowest common multiple = 21. Therefore, multiply the top pair (emeralds and diamonds) by 3, and the bottom pair by 7″
  
  Emeralds : Diamonds = 6 : 21
  Diamonds : Rubies = 21 : 14
  
  Now we can put all three stones in one row (because diamonds in both cases equals 21).
  
  Emeralds : Diamonds : Rubies = 6 : 21 : 14.
  
  Hope that helps set up the question!
  
  Reply
  1. Yamil
    
    September 16, 2013
    
    Chris Lele you are the best!!! it really help me out to understand better I hope I can get the others exercise. I practiced last night to 3 am and I could not get through it much. Now with your help I will face the others exercises I hope i can make it this time.
    
    Thank you
    
    Reply
    1. Chris Lele
      
      September 17, 2013
      
      Thanks Yamil for the kudos! I am happy the explanation helped — even if it was in the middle of the night :).
      
      Reply
  2. raquel
    
    July 27, 2015
    
    hey Chris. These are awesome posts. I just have a couple of questions on number 1, especially on what you explained to the other chris on september 16th, 2013. I understand that you have to make a similar denominator, which is 21, but why do you have to multiply one row by 3 and the other by 7? I get that 3 and 7 are the multiples of 21, and those are the diamonds and that that is the only thing we have in common in this problem, but why multiply these factors to these rows? for what?
    Also, before you stated that if we were capable of doing the first 3 problems than we have an “ok” understanding of ratios. So if I was’t even capable of doing the first one, doesn’t that say something? :/ where am i slacking? or where can i find simpler problems so that i can proceed to the first one with more ease…
    Thanks again Chris, you guys are great!
    
    Reply
adam

May 23, 2013

Thank you Tom!

The table method works great in every ratio problem. you helped me a lot!

Reply
Ve

April 9, 2012

For the question 5, can we solve it this way:
R:0:Z= unknown:2:5 = 36.
We subtract each of the option from 36 and see whether the resultant is perfectly divisible by 7. if it is not, then that is the answer.
In this case , when we subtract option b from 36, we get the output of 24 which is not perfectly divisible by 7.
Therefore, answer is B

Reply
1. Chris
  
  April 9, 2012
  
  Hi Ve,
  
  Yes, that is a good way of doing it :).
  
  Reply
  1. Anki
    
    July 26, 2013
    
    Hi Chris,
    I haven’t understood question no 5. Can you please explain it once again? The entire sum..?
    
    Reply
    1. Chris Lele
      
      July 30, 2013
      
      Hi Anki,
      
      When we have a ratio, we want to make sure to differentiate between the ratio and the sum. For instance, if the ratio of gems is 2:2:5, the total is still going to be 36. But that doesn’t mean the number of gems is 2, 2, and 5. You will have to multiply each by 4, to get 8, 8, and 20 stones, which equals 36.
      
      Of course with this problem there are various combinations that you have to figure out, besides the 2:2:5. For instance, the ratio can also be 2:5:5, 2:5:11, and 2:5:29. The final ratio actually equals 36, which means there are 2, 5, and 29 gems.
      
      Hope that helps!
      
      Reply
2. Jeet
  
  December 24, 2015
  
  Thank you
  
  Reply
Jim

February 24, 2012

Yes, I believe the last vid is a repeat of #4, and I am stuck on #5. Thanks.

Reply
1. Chris
  
  February 24, 2012
  
  I’ve added in the 5th video, I hope it helps!
  
  Reply
ingodwetrust85

February 23, 2012

Hi,
Thank you for these great explanations! However, I notice that video #4 and #5 are the same exact videos.

Reply
1. Chris
  
  February 24, 2012
  
  It’s been fixed, you can watch the explanation for the 5th video now. Thanks for letting me know!
  
  Reply