Don’t be fooled by the name! Complex numbers are not so complicated once you figure out how to deal with them. They are sometimes called imaginary numbers and are represented by the variable letter i, which is equivalent to the square root of -1.
There are only a limited amount of ways you can be tested on this topic, so cementing this knowledge in your head is a great way to win some easy points on the test. After reading this guide, you’ll be doing a fist pump each time you see a complex numbers problem on the new SAT.
New SAT Math: Simplifying Complex Numbers
On the test, you might see large negative numbers within a radical. If you take a glance at the answer choices and see that they are littered with i’s, chances are good that you need to simplify in order to get to the right answer.
For example, let’s take a look at the square root of negative 36.
In order to simplify this, use the imaginary letter i to take the negative out of the radical. Then reduce the radical down even further if possible.
This leaves us with 6i.
New SAT Math: Simplifying Fractions With Complex Numbers
When dealing with fractions, it is customary to make sure that you don’t leave any imaginary numbers in the denominator. If you have any stray i’s hanging there, multiply the numerator and denominator by i in order to get rid of it.
If you have something more complicated in the denominator, such as 3 + 4i, then you will need to multiply the top and bottom of the fraction by something called the conjugate. Don’t worry about the name; all you have to do is take the exact same numbers and flip the sign (from addition to subtraction or vice-versa).
In this case, the conjugate of 3 + 4i is 3 – 4i.
New SAT Math: The Powers of Complex Numbers
You will need to know how to reduce a power of i down to its simplest terms. You don’t need to memorize this chart, but it’ll help speed up the process so that you don’t have to think about it if you need it during the test.
i = i
i^2 = -1
i^3 = -i
i^4 = 1
i^5 = i
Since the pattern repeats in sets of 4, all you have to do is divide i’s power by 4 to figure out what it reduces down to. For example, if the quotient ends in .5, you know that it reduces to -1.
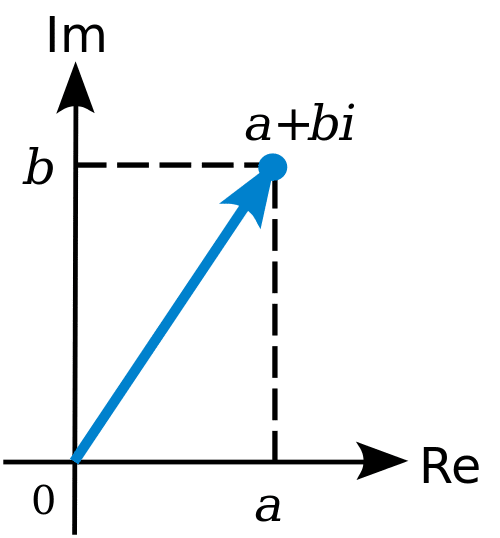
New SAT Math: Complex Numbers on a Coordinate Plane
Plotting imaginary numbers on a complex coordinate plane is a piece of cake. The x-axis represents the real numbers while the y-axis represents the imaginary numbers.
For example, (3, -4i) lies on the same position as (3, -4) on a coordinate plane. Another way of representing (3, -4i) is 3 – 4i.
In order to find the magnitude (the distance from the origin to the coordinate) of a complex coordinate, simply use Pythagorean theorem to calculate the length of the diagonal side (starting from the origin). Thus, the magnitude of (3, -4i) is 5.






Leave a Reply