What is a limit? This is a question I often hear from calculus students. The limit notation can be confusing at first, and it seems that every limit problem requires a different method. In this short article, I’ll explain the concept of a limit and how to find them in a few different cases.
Approaching the Limit
Suppose y = f(x) is a function. Informally, a limit of f is a y-value that f(x) approaches as x approaches some specified number a. We use the following notation for limits:
![]()
This notation means that f(x) approaches a limit of L as x approaches a. In the graph shown below, we can see that the values of f(x) seem to get closer and closer to y = 2 as x approaches 3.
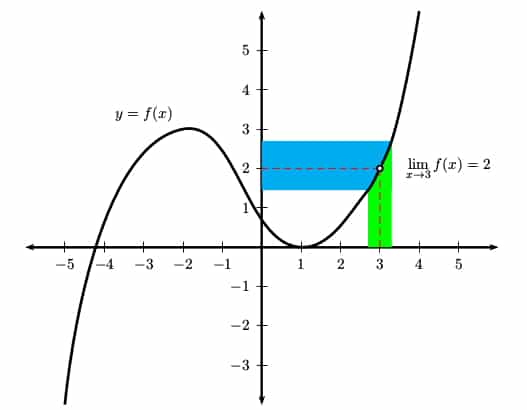
Trends in the Data
It’s important to realize that a limit problem is not really asking for the actual value of f at x = a. Instead, it’s about what happens near x = a. Based on the y-values at points near a, what would you expect the value at a to be?
The situation is a bit like finding a trend in the data. Suppose you recorded your quiz grades over the semester and found that the first 5 of them were: 74, 75, 77, 79, 80. What is the trend? The grades seem to be close to each other but rising. So you might expect the 6th quiz grade to be somewhere in the low 80s, right? You would not expect a 62 or a 99.
For example, let’s look at the graph below. What is ![]() ?
?
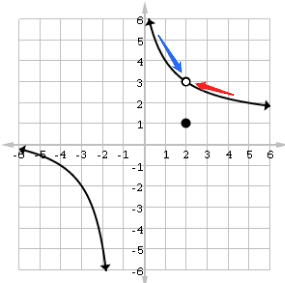
As the arrows suggest, the limiting value is 3. This is because the curve seems to lead into the point (2, 3) from both the left and the right side. Even though (2, 3) is not on the graph (that’s what the open circle signifies), and even though f(2) = 1 (that’s what the detached dot is telling us), we say that the limit as x approaches 2 must be equal to 3.
Finding Limits Algebraically
Okay, so what if we don’t have a graph in front of us? How can we find a limit of a given function? I’m glad you asked! There are many different techniques that may work on different kinds of limit problems.
If f(x) is continuous at x = a, then you can simply plug in and evaluate f(a). Many kinds of functions are continuous on their natural domains, including polynomials and rational functions.
On the other hand, sometimes a function can be undefined at a given point and yet the limit still might exist there. In those cases we must be extra careful. It may take some algebraic manipulation to rewrite the given function first.
Here is an example in which we factor and cancel before plugging in. If you tried plugging in x = 1 at the beginning, you would get 0/0, which is meaningless.
![]()
What’s Next?
Of course this is just the tip of the iceberg. For more about limits, check out
AP Calculus Exam Review: Limits and Continuity and
Limits on the AP Calculus Exam.




Leave a Reply