Warm-up: Keeping with the theme of volume of solids of revolution, try this multiple choice question, which should need only understanding of the geometric meaning of the definite integral as a measurement of volume.
Question: A solid is generated by revolving the region enclosed by the function 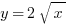 , and the lines x =2, x =3, y =1 about the x-axis. Which of the following definite integrals gives the volume of the solid? (Hint: Draw a picture)
, and the lines x =2, x =3, y =1 about the x-axis. Which of the following definite integrals gives the volume of the solid? (Hint: Draw a picture)
Calculating the Antiderivatives of an Integrand
When we look at an integral 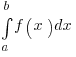 we call the values a, b the bounds of integration, while we call the function f(x) the integrand. The goal when computing an integral is to first compute an antiderivative F(x) for the integrand, for then the fundamental theorem of calculus will allow us to evaluate the right side of
we call the values a, b the bounds of integration, while we call the function f(x) the integrand. The goal when computing an integral is to first compute an antiderivative F(x) for the integrand, for then the fundamental theorem of calculus will allow us to evaluate the right side of 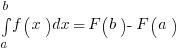 , which is much easier to evaluate than taking a limit of Riemann sums as discussed in the previous post.
, which is much easier to evaluate than taking a limit of Riemann sums as discussed in the previous post.
Therefore we need to learn how to compute antiderivatives in order to learn how to compute integrals.
The method for computing antiderivatives of a function f(x) usually consists recognizing it as the derivative of some function that you know F(x).
We need a little background now, because we are going to develop a toolkit for computing antiderivatives. A set is an unordered collection of objects. We can describe the elements of set inside of curly brackets: The integers 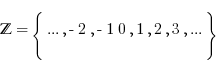 , , the real numbers
, , the real numbers 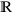 are everything in between. When there are no bounds of integration on an integral, we call
are everything in between. When there are no bounds of integration on an integral, we call 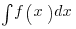 an indefinite integral. The indefinite integral of a continuous function is the set of antiderivatives for the integrand so
an indefinite integral. The indefinite integral of a continuous function is the set of antiderivatives for the integrand so 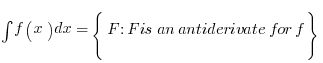 (the set notation is read as “the set of F such that F is an antiderivative for f.”
(the set notation is read as “the set of F such that F is an antiderivative for f.”
So there is more than one antiderivative for a continuous function f? Actually, the number of antiderivatives for a continuous function is actually uncountable, and certainly infinite. To see this we need two laws for derivatives: The derivative of a sum of differentiable functions is the sum of the derivatives, and the derivative of a constant function is 0. Recall that a function f(x) is differentiable if the limit ![]() exists for every point x in the domain of f, and we write this value as f'(x).
exists for every point x in the domain of f, and we write this value as f'(x).
Let f(x), g(x) be differentiable functions, then we can see using the definition of the derivative that
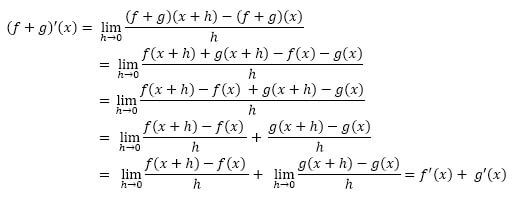 Next, we want to suppose that our function
Next, we want to suppose that our function 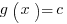 for some
for some 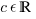 i.e. for some real number c,) then the derivative is zero at every point x:
i.e. for some real number c,) then the derivative is zero at every point x:
![]() Now we see why there are so many antiderivatives of an arbitrary continuous function f(x): Let F(x) be any antiderivative of f(x). This means that F'(x) = f(x) for every x in the domain of f. But then F(x) + c where c is a real number is also an antiderivative for f , since we have that
Now we see why there are so many antiderivatives of an arbitrary continuous function f(x): Let F(x) be any antiderivative of f(x). This means that F'(x) = f(x) for every x in the domain of f. But then F(x) + c where c is a real number is also an antiderivative for f , since we have that
Where the first equal sign uses the sum rule for derivatives and the second equal sign uses the fact that the derivative of a constant function is zero.
Therefore we write that the indefinite integral of a continuous function is a set of antiderivatives that differ by a real constant:
Solution to warm-up: A
Calculating the Antiderivatives of a Polynomial
Warm-up:
(Find the solution at the conclusion)
Today we want to discuss the computation of the antiderivatives of a polynomial function. Polynomials, as you might recall, are sums and differences of different powers of the independent variable. Some functions that are polynomials:
Some functions that are NOT polynomials:
Notice that H, G, are very similar functions to h, g, so it is important to verify if you are dealing with non-polynomial functions (like 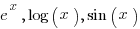 ) or simply constants (like
) or simply constants (like 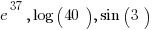 ). We now want to understand how to compute the indefinite integral of one of these polynomial functions—which means finding antiderivatives of polynomial functions.
). We now want to understand how to compute the indefinite integral of one of these polynomial functions—which means finding antiderivatives of polynomial functions.
In order to understand antiderivatives, we must first understand derivatives—so the first question we ask is:
What is the derivative of the function f(x) = 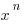 ?
?
We can answer this question by computing the limit from the definition:
Now what is 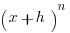 ? If we recall the binomial formula (and Pascal’s triangle) we see that
? If we recall the binomial formula (and Pascal’s triangle) we see that ![]()
Substituting this back into the limit we see that:
Since all the terms in the numerator have a power of “h”, then we can cancel and are left with:
Now since the only term without an “h” is the first term, when 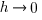 we see that all that we are left with is
we see that all that we are left with is 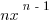 . Therefore we have that
. Therefore we have that
We now have figured out the derivatives of all sorts of functions! We have that 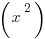 ‘ =
‘ = 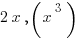 ‘ =
‘ = 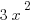 etc. The last pieces of information that we need to know, which I will not prove because it requires advanced structures, is that the integral of a sum of continuous functions is the sum of the integrals. Therefore if f(x), g(x) are continuous:
etc. The last pieces of information that we need to know, which I will not prove because it requires advanced structures, is that the integral of a sum of continuous functions is the sum of the integrals. Therefore if f(x), g(x) are continuous:
and given a real number and a continuous function f(x), the integral of (c.f)(x) is c times the integral of f(x):
This allows us to compute the integral of a sum of polynomial functions, since computing the integral will consist of finding antiderivatives for each term in the sum and then adding them together. This means we only need to know the antiderivative of 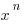 . Since a polynomial takes the form
. Since a polynomial takes the form 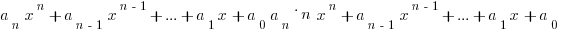 , where the
, where the 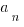 is a sequence of real constants, we can compute the integral of one as follows:
is a sequence of real constants, we can compute the integral of one as follows:
So what is the function F that is an antiderivative of 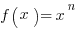 ? It will have the form
? It will have the form 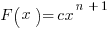 , and we can solve for by differentiating, so that
, and we can solve for by differentiating, so that 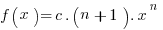 . Therefore we have that
. Therefore we have that
Therefore the antiderivatives for 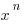 are as follows:
are as follows:
where c is an arbitrary real constant.
Warm-up Solution: C



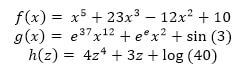
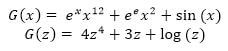
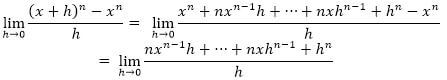
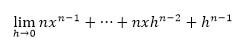
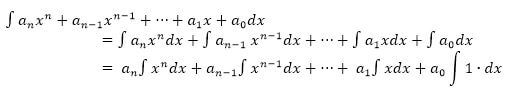
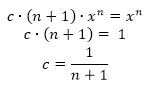
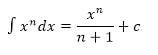

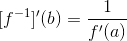


Leave a Reply