Ah, ACT Trigonometry. I can hear your reactions from here, my lovely Magooshers. “Oh, wow, trigonometry is one of the ACT math topics tested? Let me do my best cheerleader cheer! Cosine, secant, tangent, sine, 3.14159! Goooo Trig! Woo-hoo!”
Okay, I know most of you aren’t reacting that way (…yet), but I promise you’ll quake in fear just a little less when this is all over.
Trig is definitely the most intimidating math to most ACT students – that’s because most of them haven’t seen it before (or if they have, usually only in a cursory way). The good news: if you can memorize 1 acronym, 2 formulas, and 1 definition, you’ll be all set to tackle even the hardest problems!
Table of Contents
- First of All: What Is Trigonometry?
- The Basics of Trig for ACT Math
- Practice with SOHCAHTOA on ACT Math
- Reciprocal Trig Identities
- Some Helpful Hints for ACT Math Trig
- Practice Makes Perfect
- Graphing Sine, Cosine, and Tangent
- Sine, Cosine, and Tangent Graphs in Practice: Transformations
- The Unit Circle
- ACT Unit Circle Practice
Note: for more helpful math formulas, including ones for trigonometry, look here
First of All: What Is Trigonometry?
Trigonometry is the field of math that deals with triangles–specifically, the relationships between the three sides and the three angles that make up every triangle. ACT Trig is primarily concerned with right triangles. If you like right triangles, you’re going to do well here.
And typically the first thing you study in a trig class are right triangles:
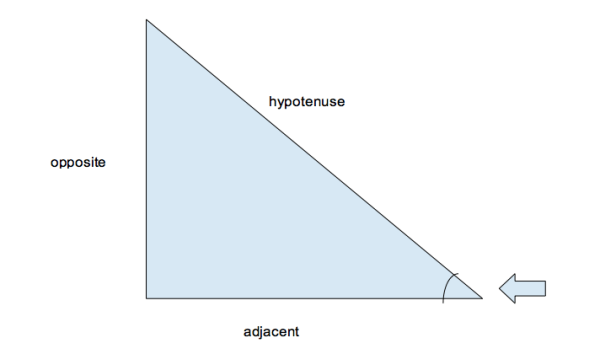
So here’s a right triangle. Let’s say that we are looking at the angle the arrow is pointing to. The side next to it is the adjacent side, the side opposite it is the opposite side, and the hypotenuse is, of course, the hypotenuse.
The Basics of Trig for ACT Math
To help illustrate my next point, let me tell you a brief story.
Once upon a time, there was a young man. He wanted to practice his baseball skills, so he started with throwing and catching. First he threw golf balls high into the air to see how high he could throw them without missing a catch. After a while, he got quite good at throwing golf balls, so he moved on to tennis balls. Once he felt confident enough with tennis balls, he moved to actual baseballs. Again, he became quite skilled at throwing baseballs, and decided to practice with bowling balls to keep improving his arm.
Of course, throwing bowling balls straight up into the air is not, generally speaking, standard practice for an aspiring baseball player, and he dropped the bowling ball directly onto the big toe of his right foot. He went to the hospital and met a lovely German doctor who told him that, luckily, his toe wasn’t broken, but he would have to take care of himself until he healed completely. He asked the doctor what he should do to take care of his foot. The doctor replied, “You must SOHCAHTOA.”
I know, I know, that was terrible. I hang my head in shame for the awfulness of that joke. But seriously, SOHCAHTOA is the answer to your trigonometry fears. It is an acronym that tells you everything you need to know to figure out basic trigonometry problems. It means:
Sine = Opposite / Hypotenuse (SOH)
Cosine = Adjacent / Hypotenuse (CAH)
Tangent = Opposite / Adjacent (TOA)
So, if you were looking for the cosine of a particular angle, you would take the value of the adjacent side to the angle and divide it into the value of the hypotenuse. Remember to keep things from the right point of view. Opposite always means “opposite to the angle you’re being asked about” and adjacent always means “next to the angle you’re being asked about.”
Practice with SOHCAHTOA for ACT Math
Example 1:
What is the sin of A?
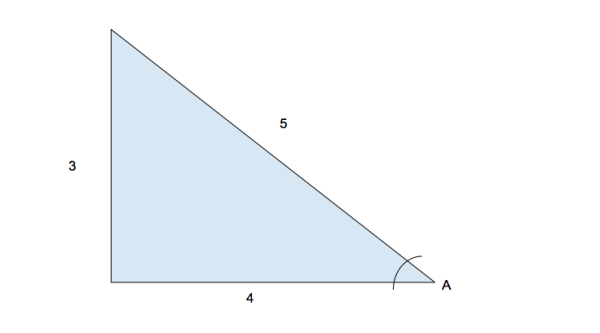
Knowing SOHCAHTOA, you would be able to answer that it is opposite/hypotenuse or 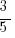 . Easy as that!
. Easy as that!
Example 2:
What is the length of XZ?
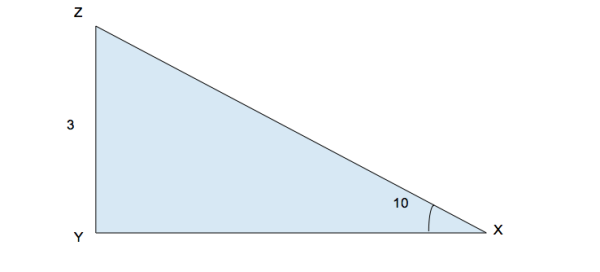
Knowing SOHCAHTOA means that if we are given a right triangle with one known length and one known acute angle (meaning not the right angle) we can always find the other two lengths.
So in this case we can use sine to find the length of the hypotenuse.
sin(10) = 3 / XZ
XZ = 3 / sin (10)
We can divide sin of 10 degrees by 3 in our calculator to get the answer: approximately 17.28.
Example 3
Here’s one that’s just a teensy bit harder, but we are just going to apply the same principles.
The tree below casts a shadow that is 24 feet long, and the angle of elevation from the tip of the shadow to the top of the tree has a cosine of 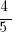 . What is the height of the tree?
. What is the height of the tree?
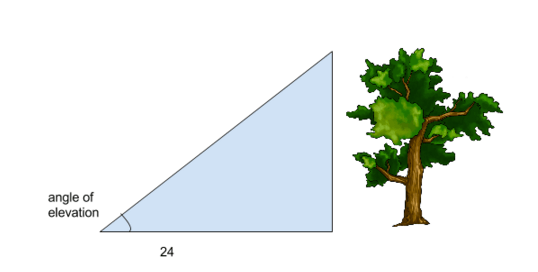
The problem tells us that the cosine of the angle of elevation is 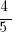 . Remember SOHCAHTOA, so we are concerned with the adjacent side over the hypotenuse. The fact that the cosine is
. Remember SOHCAHTOA, so we are concerned with the adjacent side over the hypotenuse. The fact that the cosine is 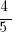 means the ratio of the adjacent side to the hypotenuse is
means the ratio of the adjacent side to the hypotenuse is 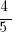 . So we can set up a proportion:
. So we can set up a proportion:
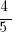 =
= 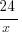
Cross-multiplying to solve for x gives us x = 30.
But remember that this is the hypotenuse and we need to find the length of the vertical side to find the height of the tree. We can use the Pythagorean Theorem to find the length of the vertical side.
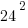 +
+ 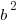 =
= 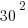
=18
So the height of the tree is 18 ft.
If you recognized that we had a 3-4-5 triangle in the beginning, you could actually take a shortcut and just use tangent of the angle of elevation to figure out the height.
Reciprocal Trig Identities
You will definitely encounter questions that require you to use SOHCAHTOA, and you may encounter questions that ask about reciprocal trig identities. Each of the three basic trig identities has a corresponding reciprocal trig identity:
Cosecant = Hypotenuse / Opposite
Secant = Hypotenuse / Adjacent
Cotangent = Adjacent / Opposite
Notice how Sine and Cosecant are the same except the numerator and denominator is flipped. That’s what we mean by reciprocal. It’s easy to remember that “tangent” and “cotangent” are reciprocals since they sound so much alike, but how what about the other two? I once had a math teacher who used, “Co-co no go” as a mnemonic device to help my high school class remember. What he meant was that your brain may think that “cosine” and “cosecant” are reciprocals since they both begin with the prefix “co-“ but that isn’t true. “Sine” goes with “cosecant” and “cosine” goes with “secant.”
Some Helpful Hints for ACT Math Trig
Let’s revisit our lovely little triangle:

You should know that you can do this:

This is what’s called the law of sines. Usually, if you have to use this formula, the question will give it to you, but it’s a handy tool to have in your pocket.
Next up is a nifty little equation that you can use on any angle. We’ll follow mathematical convention here and use the symbol θ (pronounced “theta”) to stand in for the value of the angle.
![]()
To translate from math back into English, the sine of any angle, squared, plus the cosine of any angle, squared, equals 1. Could be useful if you’re trying to figure out a tough problem on test day, no? If you see this equation anywhere on your math test, just remember that it’s equal to 1.
And to round out our helpful hints, here’s one last equation for you:

Translation: The tangent of any angle equals the sine of the angle divided by the cosine. So if a problem ever asks you to divide the sine by the cosine, you can just plug the tangent right in! (And you can figure out the value of the tangent by using SOHCAHTOA!) Easy!
To recap, let’s look at the equations all in one place:
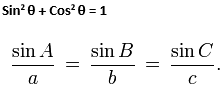
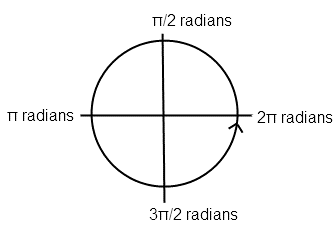
Finally, an unusual definition to learn! A radian is another way of measuring an angle. Some harder problems on the ACT will use radians instead of degrees.
There are 2π radians in one circle. Each point on a circle corresponds to a certain number of radians.
This is used in Trig to determine the location of the right triangle (and thus the negative or positive values of the sides). For example, if a Trig question told us that angle theta is between 3π/2 and 2π, we know that the angle must be in the 4th quadrant of the circle.To convert degrees to radians, simply multiply by π/180.
Practice Makes Perfect
With all of this in mind, let’s do a sample problem!


The correct answer is… D! Let’s walk through it.
To find the sine of ∠A, you need to know the values of the opposite side (line BC) and the hypotenuse (line AC). You know the hypotenuse is 8, but the problem didn’t give you a value for line BC. It did give you line AB, though, which is 6. So we can use the Pythagorean Theorem to figure out line BC!
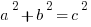 is the Pythagorean Theorem, as you might recall from the review on triangles. Substitute in the values we know, and it becomes:
is the Pythagorean Theorem, as you might recall from the review on triangles. Substitute in the values we know, and it becomes:

Now that we know the value of line BC, we can figure out the sine of ∠A.

Graphing Sine, Cosine, and Tangent
These graphs are usually graphed and expressed in degrees, but you may also see them expressed in radians.
Sine and cosine both have standard graphs that you need to memorize for the ACT Math Test. The standard equation for sine looks like this: y = sin x. The “period” of the wave is how long it takes the curve to reach its beginning point again. The coefficient in front of “sin” (here 1), is called the amplitude. It effects how high and how low the wave reaches vertically. If that coefficient changes, then the height changes. For example, y = 5 sin x, would show a curve that reaches +5 on the y-axis and extends down to -5 on the y-axis.
Cosine also has a standard equation. It looks like: y = cos x. For the graph of cosine, notice how it begins at its highest y-value and descends, whereas sine begins at the origin. Cosine and sine have the same period of 2π. Questions involving trig graphs will likely require you to match given equations with graphs, or interpret the meaning of certain graphs, such as in a question like this: What is the smallest positive value for x where y = cos 2x ?
The difference between y = cos x and y = cos 2x is that the coefficient in front of x is halving the period, so it will now take just one pi to complete its cycle. The smallest x-value for cosine usually occurs at π/2. For the new graph, it will occur at π/4, which is ½ of π/2.
Confused? Want more? Kristin’s here to explain!
Sine, Cosine, and Tangent Graphs in Practice: Transformations
The ACT may also ask you to transform, or change, the equations and then explain what happens. Using sines as our example, let’s take a quick look:
- The graph of y = 2 sin x increases the amplitude of the wave, meaning the waves are taller.
- The graph of y = ½ sin x decreases the amplitude of the wave, meaning the waves are shorter.
- The graph of y = sin 2x decreases the period of the wave, meaning the wave peaks are closer together horizontally.
- The graph of y = sin ½ x increases the period of the wave, meaning the wave peaks are farther apart.
What does that look like in practice? So glad you asked…
How will the graph of the function f(x) = 4sin x + 0.2 differ from the graph of f(x) = sin x?
A) The graph’s period will be 4 times as much and the graph will shift 0.2 units down.
B) The graph’s period will be 4 times as much and the graph will shift 0.2 units up.
C) The graph’s amplitude will be 4 times as much and the graph will shift 0.2 units down.
D) The graph’s amplitude will be 4 times as much and the graph will shift 0.2 units up.
We know that the coefficient in front of sine changes the amplitude, so (A) and (B) can quickly be eliminated, since 4 multiplies the amplitude by 4. Just like a linear equation, adding to the end of an equation shifts a graph upwards. For example, the only difference between y = 8x and y = 8x + 7 is that the latter is 7 places higher on the y-axis. The answer is (D).
The Unit Circle
Now, let’s take a look at the famous unit circle: a cool little circle that is often featured on ACT trig questions, so it’s a must-know ACT math thing.
THIS is a unit circle. It’s a circle with radius of 1 centered about the origin.
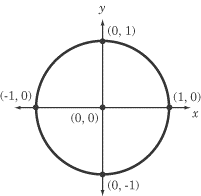
There are a lot of fascinating aspects to the unit circle: I suggest you consult the interwebs or your math teacher to find out more. We’re just going to go through the absolute basics here that will help you get some ACT trig questions right.
The ACT will test whether you know where angles larger than 360 degrees lie, and the unit circle helps us visualize this.
There are 360 degrees in a circle, but we can just keep swinging the arm of the angle around counterclockwise (just like the hands of the clock) to get to an angle bigger than 360. So, for example, if you want to know where an angle of 760 would be, you would circle around the circle twice (for a total of 720 degrees) and we would have 40 leftover degrees. So that angle would lie in the upper right quadrant of the unit circle (Quadrant I).
The ACT will also often use radians on trig questions, and the unit circle helps us wrap our heads around this.
You should know that:
90 degrees on the circle = π/2
180 degrees = π
270 degrees = 3π/2
360 degrees =2π
The ACT will also test whether you know where the sine, cosine, and tangent of angles are positive or negative on the unit circle.
Check out the video below for the actual math explanation of why sine, cosine, and tangent are positive or negative in certain quadrants!
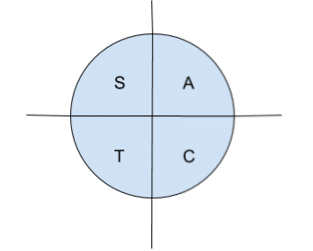 There’s a great mnemonic to help you remember where trig functions are positive or negative:
There’s a great mnemonic to help you remember where trig functions are positive or negative:
All Students Take Calculus
This helps you remember that:
In Quadrant 1 → All (sine, tangent, cosine) are positive
in Quadrant 2 → only Sine is positive (and cos and tan are negative)
in Quadrant 3 → only Tangent is positive (and sin and cos are negative)
in Quadrant 4 → only Cosine is positive (and sin and tan are negative)
ACT Unit Circle Practice
Now let’s look at a test example to show you how this helps you out on a frequently-occurring ACT question:
If the value of cos x = -0.385, which of the following could be true about x?
- A. 0 ≤ x < π
- B. π/6 ≤ x < π/3
- C. π/3 ≤ x < π/2
- D. π/2 ≤ x < 2π/3
- E. π/3 ≤ x ≤ 2π
Using ASTC (All Students Take Calculus), we can figure out where cosine is negative and narrow down our answer choices. Cosine is negative in Q2 and Q3 and positive in Q1 and Q4. So we can eliminate any values that would fall in either Q1 or Q4. Answer choices A, B and C all have values that fall in Q1. Answer choice E is Q4. So that means the answer HAS to be D because that is the only answer choice in Q2 where cosine is negative. (And yes, it often is as easy as that on the ACT!)
For more on unit circles, check out Kristin’s video explanation here:
Looking for more problems to polish your skills? Check out these ACT math practice problems!






Leave a Reply