There will be a number of times on your SAT when you’ll be asked to find the measurement of an angle or angles, but you’ll be given a picture with only a bit of information on it.
In these questions, the SAT makers are testing you on your ability to move information around a figure. If you know that one angle is 40˚, for example, can you find any other equal angles? Any complementary angles (adding to 90˚) or supplementary angles (adding to 180˚)?
In order to answer this type of question, you’ll need to know some basic geometry facts. Some are at the beginning of each math section, and some aren’t.
Fill in every angle you can
If you’re asked to find the measurement x of an angle, you may not immediately see how to get there. That’s fine. Just start putting in the measurements that you do know, and you’ll find that some helpful information starts to pop up. Take a look at the example figure below, and see if there’s anything you can add to it.
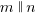
Knowing a thing or two about triangles and parallel lines makes this a pretty easy figure to work with. From that given 45˚ angle, we can write in the measurement of its opposite, which is also 45˚. Or we can move it to the corresponding angle on line n. We can write in three other 45˚ angles altogether.
If you wanted, you could actually find every angle on here pretty quickly; it’s not necessary to start with the 45˚. You could also start from that right triangle, which is a 30˚-60˚-90˚ triangle. (By the way, that should set off a little alarm bell in your head—if the question asks about the lengths of any segments, you can definitely use that information).
By writing the 60˚ into that angle of the triangle, you’re pretty much there. Moving that around to as many places as you can along with using the 45˚ angle (or it’s supplement, 135˚) will bring you to a point where you can say that x must be 75˚.
Focusing on the goal measurement for the answer
If you see relationships that will bring you toward your answer right away, then by all means, don’t waste the time writing in unnecessary angle measurements. But analyzing the figure in your head is sometimes a tough thing to do: writing in the info that you do know will direct you toward the path you need to take.







Leave a Reply