Unlike the SAT, the ACT does not provide you with a list of basic math formulas to rely upon at the beginning of the ACT math test. This means you will need to be able to recall math formulas on the ACT. Below you will find lists of “Must Know” ACT math formulas, “Good to Know” formulas, and “Bonus” formulas to commit to memory for the ACT! Learn them all, then check out our list of ACT math topics to begin applying them!
Must-Know ACT Math Formulas
Though the ACT tests different concepts on each exam, there are popular topics (like ratios!) that come up again and again. This list contains the best ACT math formulas to know. For more practice, try these ACT math practice questions, then check out Magoosh ACT prep.
Average
- S/T (Average = Sum/Number of things)
Lines
-
- Slope intercept form:
y = mx + b (where m is the slope and b is the y-intercept)
-
- Slope:
![]()
Triangles
-
- Area of a triangle:
1/2bh (1/2 base × height)
- Pythagorean Theorem:
a2 + b2 = c2
Quadrilaterals
-
- Perimeter of a rectangle:
2l + 2w (where l is the length and w is the width)
-
- Area of a rectangle:
lw (length × width)
-
- Volume of a box:
lwh (length × width × height)
-
- Surface area of a rectangular solid:
2lw + 2wh + 2lh
-
- Diagonal in a rectangular solid:
Apply the Pythagorean theorem twice or l2 + w2 + h2 = d2
Circles and Spheres
-
- Area of a circle:
πr2
-
- Circumference of a circle:
2πr
-
- Volume of a sphere:
4 / 3πr3
Cylinders
-
- Volume of a cylinder:
πr2h
Trigonometry
-
- SOHCAHTOA:
sin x = opposite/hypotenuse
cos x = adjacent/hypotenuse
tan x = opposite/adjacent
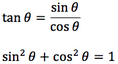
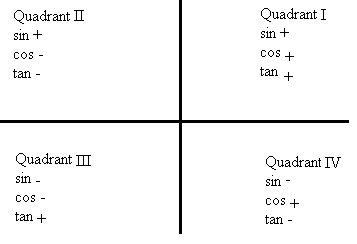
- You should also know your quadrants and where sine, cosine, and tangent are positive or negative:
Probability
-
- Probability:
Number of desired outcomes / number of total outcomes
-
- Factorials (e.g. 8!):
To find the factorial of any integer, multiply it by every positive integer below it, e.g.:
8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Bonus: the “Must Know” math formulas on the ACT also appear in your high school math classes. So, you’re really studying for two things at once. Nice.
Bonus bonus: Check out the video below to watch ACT expert Kristin discuss 6 of the must-know ACT math formulas in greater detail:
ACT Formulas that are Good to Know
Volume and Area
-
- Volume of a cone:
V = 1/3πr2h
-
- Volume of a pyramid:
![]()
- Area of a trapezoid:
![]()
(Add the bases, divide by two, then multiply by the height.)
Logarithms
-
- Definition:
If logab = c, then ac = b
- Change of base rule:
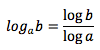
Triangles
-
- 30-60-90 Triangle Ratio:
1 : 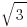 : 2
: 2
-
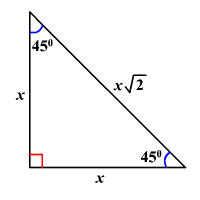
- 45-45-90 Triangle Ratio:
1 : 1 : 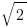
Additional Formulas
-
- Equation of a circle:
(x − h)2 + (y − k)2 = r2 (where center of the circle is (h,k))
-
- Arithmetic sequences:
tn = t1 + d(n − 1)
-
- Geometric sequences:
tn = t1 × r(n − 1)
-
- Exponential Growth Formula:
![]()
Where P = principal (starting value), r = rate of growth, n = number of months, t = time in years, and A = new amount.
Bonus Things to Know
-
- Quadratic Equation:
![]()
Often, you will be better off applying a strategy such as backsolving to solve a complicated algebra problem, but if you are comfortable with the quadratic equation, keep it in the back of your mind.
-
- Permutations:
![]()
- Combinations:
![]()
An Important Note About ACT Math Formulas
Occasionally, an ACT math problem may rely upon a more advanced formula, such as the surface area of a sphere. In these cases, the question itself will typically provide you with the formula you need. So no need to think you need to memorize everything. However, being able to recall basic formulas will ensure you can tackle problems that don’t provide a formula with confidence! The list below includes formulas for the concepts the ACT tests most frequently.
Important ACT Math Formulas to Know (PDF)
Sometimes it’s easier to memorize formulas by studying a little bit every day. To make this easier, we created a printable Magoosh ACT Math Formulas PDF. Here’s the link where you can get your copy.

Let us know if you have any questions about these ACT formulas. 🙂
Image Credit: hotmath.com and getmathhelp.jimdo.com
Need more help?
With Magoosh ACT, you can choose between a live cohorted class with an instructor (which includes all our lessons and practice questions) or access to the self-study option by itself.





Leave a Reply