Probably not. Meaning that parabolas can show up on the GRE, but probably won’t show up on the GRE you are taking. That is my initial take based on forums and students experiences. Still, parabolas, along with absolute value graphs, are included in the Practicing to Take the Revised GRE book. ETS obviously didn’t put them there to kill more trees. So, like compound interest and the quadratic equation, parabolas may show up.
What this means for your study plans is that you should only worry about parabolas if you are looking to score above 90%, and have already brushed up on the other concepts on the new GRE math. Meaning, if you are still struggling with number properties or circles, focus there.
That said, below are some important things you have to know about parabolas.
Introduction to parabolas on the GRE
Symmetry
If you draw a line dividing a parabola in the middle, the parabola will be split into two equal halves. This line is known as the axis of symmetry. The shape of the parabola to the right of the axis symmetry is identical to the shape of the parabola the left of it.
The axis of symmetry will either be a vertical line or a horizontal line, but the effect will always be the same: to split the parabola into two equal halves.
The equation of a parabola
The equation for a parabola will always contain a coefficient, meaning that x is always squared: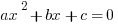 
. This may not be too helpful, so just think of it this way: 
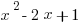, when graphed, is a parabola. On the other hand, when the x is not squared, say, 
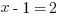, we have a simple line.
The equation for a parabola can also be written as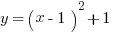 
. (This would turn out to be 
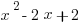if written in the format in the preceding paragraph).
This form is also known as the vertex form and is expressed as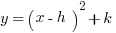 
. The reason this is call vertex form is it makes finding the vertex very easy.
So how does all of this pertain to the new GRE? Well, remember the line of symmetry? To find it, we simply look at the value of h. In the example above, we have 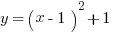, therefore h is equal to 1.
Finally, there is the vertex, which is either the highest or lowest point depending on the equation (see horizontal vs. vertical, upwards vs. downwards). The vertex can always be represented by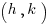 
. Since h is already 1, we need to find k. This becomes straightforward if we put the following two equations next to each other:
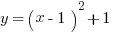and
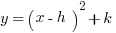
Notice that the k is in the place of the 1 on the equation to the left. Therefore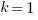 
. which is also 1. Hence the vertex.
Intersecting lines
The point at which a straight line intersects a parabola can be found by setting the equation for the line and the equation for the parabola equal to each other. If a line intersects a parabola set the two lines equal to each other.
For instance the line,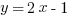 
and the parabola 
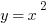, both equal y so we can set them to equal to each other: 
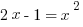. We get 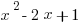, which equals 
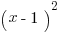. Therefore 
.
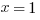To find y, we simply plug 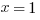into either equation (they will always be the same). The answer then is 1. So the line and the parabola intersect at 
.
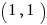Sometimes a question will simply ask you at how many points a line intersects a parabola. A line can intersect a parabola at zero points, one point, or two points.
Sometimes simply graphing out the parabola and the line is the easiest way to answer such a question.
Types of parabolas: horizontal vs. vertical, upwards vs. downwards
Let’s have a look at two different parabolas:
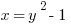
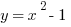
The two equations are identical, save that the x and y have been swapped. Whenever a parabola is equal to x it is horizontal, meaning that the axis of symmetry is horizontal.
When the parabola is equal to y, the axis of symmetry is vertical.
In the case of 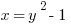the parabola opens to the right. In the case of 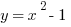the parabola opens upward.
Now have a look at the following equations:
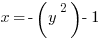
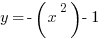
This pair of equations is identical to the ones above, except for there is a negative in front of both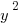 
and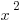 
. This negative flips the direction of each parabola.
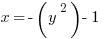opens to the left and 
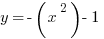opens downwards.
If this all seems very abstract take a look at the video above.
Skinny vs. fat parabolas
Finally, a parabola can change its shape depending on whether the coefficient (or number) next to 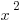is less than or greater than one. For instance, in the equation
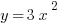the coefficient is 3, so we will have a ‘skinny’ parabola—that is, the great the coefficient the skinnier the parabola. On the other hand, in 
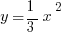, the coefficient is 
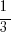so we will have a ‘fat’ parabola.
(Skinny and fat are my terms not standard math-ese. So if you whip them out in front of math inclined folk you are likely to get some very quizzical looks).
Takeaway
There is much to learn on parabolas, as you can see from the post above. However, there is little likelihood that a parabola will even show up on the test so study only if you are aiming for a top math score.
The accompanying video should hopefully make what I covered in this post far less abstract.
