Inverse Proportions on the GRE: The Flip It Method

Dealing with percent and word problems is always difficult. First off you have to understand what the question is asking for, then you have to set up what you believe is an equation that will help you quickly derive the answer.

Each of the questions below tests the following concept: if one thing increases by a certain percent, another thing will decrease by a certain percent. That is two things are in inverse proportion to each other.

To illustrate, let’s take a relatively straightforward example:

The product of positive integers b and c is 60. If b is doubled, then c must decrease by what percent so that the product of the two will still equal 60?

(A)  10

(B)  25

(C)  50

(D)  200

(E)  Cannot be determined from information given.

One way to solve this is to set up an equation:

If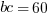

And 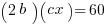, what must x equal?

Using substitutions we take bc = 60 and we plug it into the bottom equation:

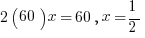or 50% (C).

You can probably see that this is an unpleasant and cumbersome approach. Nonetheless, many students feel they have to set up some equation, however unwieldy it may be. Instead, think of the above problem in the following way:

If one element doubles, then the other element must be halved in order for the product to remain unchanged. Therefore the answer is 50%.

It’s also important to note that the fact that the product is 60 is irrelevant to the problem. The product could have been any number. Don’t fall for answer (E)!

Now let’s take the concept above and apply it to a different problem.

Mike drives 45 mph to work and arrives in 20 minutes. If he wants to complete the trip in 15 minutes, how fast must he drive?

(A)  42

(B)  50

(C)  54

(D) 57

(E)  60

Solution: The logic of inverse relationships is that one number increases while the other decreases. There must also be a constant number, such as 60 in the preceding problem.

In this case, the constant number is the distance Mike drives to work. What varies is the speed and his time.

We can set up an equation (but we saw where that got us last time), or we can think of it this way—Mike wants to arrive at work at 15/20 of the time. Therefore, he must increase his speed by the reciprocal. Or as I like to say Flip It! 15/20 becomes 20/15. 20/15 x 45 = 60.

Indeed, we did the exact same on the preceding problem: 2/1 (the amount we increase b) is flipped to give us ½, the amount we decrease c by.

Practice Questions

1. If X decreases 40%, by what percent must it increase to return to its original value?

(A)  40

(B)  50

(C)  66 2/3%

(D) 75%

(E)  80%

2. Driving at a constant speed of 60/mph, Bob can reach his work in 15 min. If he wants to reach work three minutes faster, by how many miles per hour must he increase his speed?

(A)  12 mph

(B)  15 mph

(C)  20 mph

(D) 75 mph

(E)  80 mph

3. 15 workers can paint 3 fences in 2 hours. Assuming each worker works at the same rate, how long will 5 workers take to paint 6 fences?

(A)  3 hrs

(B)  6 hrs

(C)  7.5 hrs

(D) 9 hrs

(E)  12 hrs

Answers and Explanations

1. We can choose the number 100 for X. If X drops 40%, it is at 60. That is we multiply the 100 by 6/10. The flip it method shows us that all we have to do is flip the 6/10 to get 10/6. 10/6  = 1 2/3. We discount the ‘1’ because that is already the value of X after it has dropped 40%. Therefore it only needs to increase by 2/3 to reach its original value. Therefore the answer is (C) 66 2/3.

2. We are multiplying the time it takes him to get to work (15 minutes) by a number (x), which will yield 3 minutes faster (12 minutes). 15x = 12; x = 4/5. Using the flip it method, we multiply 60 by 5/4 to get 75. The question asks how much he must increase his speed by. So be careful not to pick (D), but to subtract 60 from 75, to get 15. Answer (B).

3.5 workers means that painting the fence will take 3 times as long. Because those five workers have to paint twice as many fences, we have to multiply the original time by 3 and by 2: 2 x 3 x 2 = 12, Answer (E).