Have a go at a type of difficult GRE math problem that “freaks out” (my students’ own words) test-takers: multiple-answer questions.
Which of the following must be greater than 
, where 
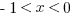? Choose ALL that apply.
This is a very difficult, time-consuming problem. Unfortunately, there will be a few such problems on the new GRE math section. The good news is that the new GRE will not have too many problems that are multiple answer questions. Out of the 20 questions on the quant section, you will only have about one or two such questions.
Choose Numbers
When dealing with variables in the answer choices, you should always plug-in your own numbers. Starting with (A), we can see that we will have a negative fraction: multiplying a negative times itself three times will yield a negative: 
. The question is will this fraction be greater or smaller than ?
Let’s plug in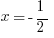 
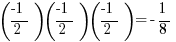
On a number line,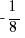 
is closer to zero than 
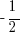. Therefore, 
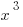will be greater than . This will hold in each case, because as you take any fraction between 
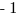and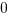 
to an odd power, you will always make this number approach zero. ONE ANSWER.
For (B), the opposite is true. Taking a cube root of a fraction between 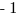and 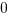will make that number more negative. At first, you may be hard-pressed to find a fraction in which you can easily take the cube root. From above, we cubed 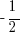to get 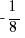. Therefore, the cubed root of 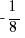is 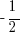. We are reversing what we did with answer choice (A); therefore, (B) will always be higher, not lower, than .
Test Both Ranges
With (C), we can plug in 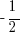for , giving us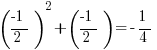 
. In this case, the answer choice is greater than . You shouldn’t stop there, but test using different numbers. I would suggest numbers closer to the far end of the range, i.e. numbers close to 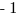or 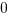. Once you’ve established that this relationship holds true at both ends of the range, in this case, 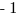is the lowest and 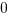the highest, then you’ve done enough plugging in and can include (C) as one of the answers. ANOTHER ANSWER.
A more logical (and optimal) approach is to note that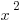 
will always be positive. Since you are adding a positive number to , which is negative, will become less negative. There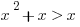 
.
Think in terms of Positive or Negative
For answer choice (D), 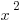has to be positive. 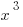is negative, but since you are subtracting this negative fraction, it is the same as adding it. Therefore, a positive plus a positive must be positive. For instance, plugging in 
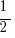for : 
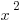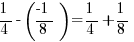is clearly positive. YET ANOTHER ANSWER.
Finally, we have answer choice (E). Let’s start with .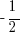
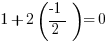
Do we stop there? Well, remember, the question is asking us for answer choices which MUST always be bigger than . Just because we found value where that is the case does not mean that it holds true for all values. Let’s plug in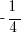 
for . We get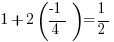 
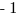What happens when we make more negative? Well, let’s work from extremes: must be less than . But let’s say is equal to 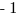. Plugging in , we get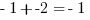 
. On the other extreme, could be zero. Here we would get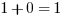 
. Therefore, the range of when we plug in into the equation must be between -1 and 1.
Final Answers: A, C, D, and E
Again, this is a very difficult problem, and you probably will only see a couple such time-consuming problems. The takeaways from this problem, however, can be applied to quantitative comparison problems that ask you to reason with fractions and negative fractions. As for quantitative comparison questions, they will comprise roughly 40% of the 20 math questions you will see on each of the Revised GRE math questions. So, make sure you are able to confidently handle thorny problems like the one above.
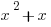
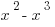
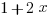
Leave a Reply