
What’s the biggest secret to GMAT math success? It’s simple! Identify and study the correct quantitative concepts, strategize for problem solving, and leave rote memorization at home. As you may already know, the two types of GMAT math problems are Problem Solving and Data Sufficiency, but what are the GMAT math topics you’ll see on test day? And which ones are the most important?
The GMAT Quantitative section consists of 31 questions in 62 minutes. It’s an adaptive test, meaning that if you correctly answer a few questions, then the next one may be more difficult. Don’t let that worry you though! This is just how the test finds your math ability level.
Furthermore, you’ll never encounter any questions that require more than a basic high school understanding of quantitative concepts. Generally speaking, the GMAT Quant section tests your abilities to analyze and problem-solve rather than any advanced knowledge of mathematics. Emphasis is placed on data interpretation, critical reasoning, and word problems.
Improve your GMAT scores with Magoosh GMAT, you can choose between a live cohorted class with an instructor (which includes all our lessons and practice questions) or access to the self-study option by itself.
Table of Contents
- What kind of math is on the GMAT?
- GMAT Quantitative Section Breakdown
- GMAT Math Tips and Practice Problems
What kind of math is on the GMAT?
There are two types of GMAT math questions: Problem Solving and Data Sufficiency. Problem Solving problems are by far the more familiar: just work out the question and choose the correct final answer.
But Data Sufficiency problems are at a higher level, literally! Instead of seeking an answer to the problem, you have to decide whether there is enough information to answer the problem in the first place.
The Four GMAT Math Areas
The quantitative knowledge necessary to ace the GMAT consists of basic high school mathematics.
- Arithmetic: Number sense, operations on numbers, etc.
- Algebra: Basic manipulation of expressions and solving equations
- Geometry: Angles, lines, and circles (and a bunch of other things)… oh my!
- Word Problems/Applications: Includes things like basic statistics. But in some ways, many of the problems on the GMAT Math section are word problems anyway. In fact, all of the word problems use arithmetic, algebra, or geometry in some way. But the emphasis here is on critical reasoning and understanding how to apply what you know from other areas of math.
Here is just a small sample of Magoosh video lessons with helpful GMAT Quant tips and strategies related to the four math areas:
GMAT Quantitative Section Breakdown
The table below lists GMAT quant concepts in order of most-to-least frequent. (The most frequent concepts are obviously the most important!) To measure the frequency of GMAT math topics, I analyzed 766 official questions from the official GMATPrep tests 3 and 4, and the Official Guide for the GMAT Review so you don’t have to!
Note, of course, that the figures below are estimates based on a large number of questions, and may not reflect the exact proportions on an individual test.
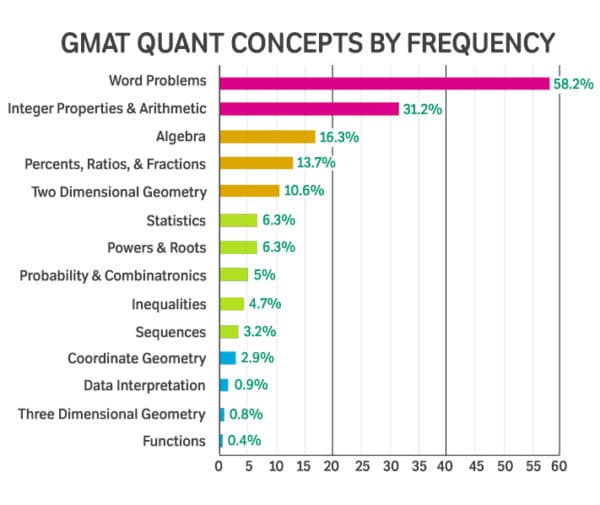
| GMAT Quant concept | Percentage frequency | What’s it about? |
|---|---|---|
| Word Problems | 58.2% | Interpreting the math in stories and descriptions |
| Integer properties and arithmetic | 31.1% | Interpreting the math in charts and tables |
| Algebra | 16.3% | Includes both “pure algebra,” and algebra as applied to other GRE quant concepts |
| Percents, ratios, and fractions | 13.7% | |
| Two dimensional geometry | 10.6% | Shapes, lines, and angles on the coordinate plane |
| Statistics | 6.3% | Mean, median, standard deviation, etc… |
| Powers and roots | 6.3% | |
| Probability and combinatronics | 5% | Permutations, total number of possibilities, odds of an event happening, etc… |
| Inequalities | 4.7% | |
| Sequences | 3.2% | |
| Coordinate geometry | 2.9% | |
| Data interpretation | 0.9% | Math problems based on tables, charts, and graphs. You will also find these in the GMAT Integrated Reasoning section. |
| Three dimensional geometry | 0.8% | |
| Functions | 0.4% |
Note: Some questions tested multiple concepts and were thus counted more than one time in more than one category. As a result, the percentages in the chart above add up to more than 100%.
- Now that you know the most frequent GMAT math questions, check out the hardest concepts and questions in our latest video!
GMAT Math Tips and Quant Practice Problems
Now let’s talk about what you can do to improve your GMAT Math score! Here are a few helpful GMAT quant tips, followed by practice problems and detailed solutions, to get you right on track toward a higher score.
Tip #1 — Rely on your Critical Reasoning; Not Deep Knowledge
The GMAT Quant problems test your ability to analyze data and draw conclusions, not advanced mathematical ability. As a result, this can actually cause the test to be very challenging for high-achieving students. You may have progressed through Calculus and beyond, but if you don’t have enough practice solving logical puzzles or real-world problems, then you’ll need to study up!
(1) The group has more than four times as many seniors as it has freshmen.
(2) The group has more than 7 freshmen.
First, what is given? There are 42 freshmen and seniors, but we don’t know exactly how many of each. Two unknowns, and one relation (equation). So we are looking for the statement(s) that can help to set up another equation if possible. Statement (1): Be careful, as the wording is tricky here. To say that the group has more than four times as many seniors as freshmen only allows you to set up an inequality (not an equation). It could be that there are zero freshman and 42 seniors, or 8 freshmen 34 seniors, or anything in between. Statement (2): By itself, this doesn’t narrow the field down either. Just saying that there are more than 7 freshmen leaves open all possibilities from 8 to 42 freshmen! But now look again at the conclusions of the two statements. Statement (1) gives you a maximum of 8 freshmen. That’s because 9 freshmen would leave 33 seniors, which is more than four times 9. And Statement (2) gives you a minimum of 8 freshmen (the first whole number more than 7). Thus, together Statements (1) and (2) are sufficient. Answer: C Both are sufficient, but neither one alone is sufficient.
Click here for the answer!
As you can see, this problem requires nothing but arithmetic and a little bit of critical reasoning. Since it’s a Data Sufficiency problem, don’t worry about trying to solve all the way to a numerical final answer. Instead, let’s go through each of the two statements one by one.
Tip #2 — Arithmetic Questions: Use Your Number Sense
The key to solving quantitative arithmetic questions is to rely on your number sense and avoid common pitfalls.
This is a typical problem dealing with units and ratios. Let’s use our number sense to quickly tackle this one. First, the fact that the price of flour is \(w\) dollars per \(x\) pounds, means that whatever the final answer is, the \(w\) and \(x\) need to be on opposite parts of the fraction. That’s because \(w\) per \(x\) means \(w/x\). So either that, or its reciprocal will be in your final answer. So that narrows it down to just two choices without much work! Either \(\frac{xy}{w}\) or \(\frac{w}{xy}\). Finally, the question is asking for the cost of making one cake. So let’s what happens if we allow \(y\) to vary. Suppose \(y\) is small, like \(y=1\). Then it takes a whole pound of flour to make just 1 cake. But if \(y\) is larger, say \(y=4\), then that same one pound of flour goes much further, bringing the overall cost down per cake. As \(y\) increases, the cost per cake has to decrease. That tells you immediately that \(y\) must be on the bottom of the fraction (in order to get that kind of inverse relationship). Answer: \(\frac{w}{xy}\)
Click here for the answer!
See, that wasn’t too hard, right? There are certainly other ways to work this kind of problem out. If you want to see more on this topic, here’s an excellent refresher for GMAT Quant: Rates and Ratios.
Tip #3 — Algebra Problems: Try Backsolving or Picking Numbers
Common strategies for algebra problems include backsolving and picking numbers. These techniques make it possible to solve a problem without actually solving it. In other words, you can avoid some of the heavy lifting of algebra if you can leverage the answer choices to your favor.
Backsolving works by using the answer choices to work backwards. Often this means plugging in each numerical answer choice into given equations, but it can also sometimes be useful when the answers themselves are equations.
Picking numbers is precisely that! It’s when you pick values for some or all of the variables in a problem, and work the problem with your choices. This often requires you to plug in your numbers into answer choices or Data Sufficiency statements to help eliminate choices.
Want to avoid the algebra? Let’s pick some convenient numbers for the variables. Keep in mind that \(m \neq n\). So, let’s start with \(m=2\) and \(n=1\). Plugging those into the given equation, we get: \(6x + 4y – 2y – 3x = 0\), which simplifies to: \(3x + 2y = 0\) Now we could even plug in a number for \(x\) and work out \(y\) from that (to compare with the answer choices), but there’s no need on such a simple equation. \(2y = -3x \implies y = \frac{-3x}{2}\) Answer: \(-\frac{3x}{2}\)
Click here for the answer!
Tip #4 — Geometry Problems: Be Goal Oriented
The hardest part about geometry problems is just knowing where to start. It helps to identify the goal and then try to work to fill in the gaps from your given information toward the goal. Think about these questions as you work out geometry questions on the GMAT Math section:
What information do I have? Where do I need to end up? What info would be useful to bridge the gap? Are there any formulas that could help?
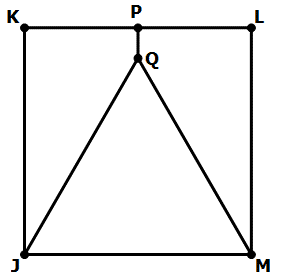
(1) \(∠KPQ = 90°\)
(2) \(∠JQP = 150°\)
What is given? JKLM is a square; P is the midpoint of KL. Where do I need to end up? Determining whether triangle JQM is equilateral or not. What info would be useful? Knowing all the angles, of course! Helpful formulas? We’ll probably need the fact that all angles in a triangle add to 180 degrees and properties of parallel lines cut by a transversal, because frankly those concepts seem to be important in almost every one of these kinds of problems. Let’s look at Statement (1). If angle KPQ is 90 degrees, then PQ would be parallel to KJ. That’s a great start, but doesn’t give enough info by itself to solve the problem. For instance, the angle JQM would vary depending on how long PQ is. Now consider Statement (2). By itself, having angle JQP is nice, but just not sufficient. What if point Q is left or right of the midline? We’d have no definite way of finding the angles of triangle JQM. However, if both Statements (1) and (2) are taken together, then you have KJ parallel to PQ, and angle JQP = 150. Then angle KJQ is equal to 30 (same-side interior angles). That makes angle MJQ equal to 60. But then because PQ is centered on the midline of the square, the other side is a perfect mirror image. And that gives you angle JMQ — 60 degrees as well. Finally, angle JQM must also be 60, and the triangle is guaranteed to be equilateral! Answer: C Both Statements (1) and (2) TOGETHER are sufficient to answer the question asked; but NEITHER statement ALONE is sufficient.
Click here for the answer!
Tip #5 — Word Problems: Don’t Get Lost!
Word problems tend to overlap with the other categories. These kinds of problems test your ability to assess a given situation, set up proper steps, choose the correct mathematical tools to solve the problem, and finally to obtain the best answer (or determine if it’s possible to do so, in the case of Data Sufficiency questions). It’s crucial that you don’t get lost. When you read a long word problem, jot some things down as you go. Pay attention to constants and constraints given in the problem. And identify your goal.
Both are sufficient, but neither one alone is sufficient. There’s a lot to keep track of here, and some info is just not that important. For example, you don’t need to know that one pump is a “JQ” and other other is a “JT” pump, just that there are two types and they run at different rates. They could have been called “A” and “B” or “1” and “2” for all we care. But it is a good idea to jot down “JQ” and “JT” on your scratch paper to start organizing the rest of the data. The JQ pump fills the tank in 72 hours. How much water is that? We don’t know. But you can say it’s 1 tank worth. So write “1 tank in 72 hrs.” in your JQ column. Similarly, put “1 tank in 18 hrs.” in your JT column. Now, it goes on to ask about filling up a half-full tank. So, alone the JQ would take 36 hours. But we have two JQ’s, which by themselves would cut that fill time to 18 hours. Finally, the trickiest part, what happens when you add in the JT? By itself, it takes 9 hours to fill half the tank. Let’s bring in our number sense. Every time unit, the JQ’s are going to fill only half as much water as the JT, because the JT is pumping twice as fast. When the tank fills, two-thirds of the water was pumped in by the JT, and only a third of it by the two JT pumps. So either way you look at it, 6 hours are needed — either one third of 18 hours, or 2/3 of 9 hours. Answer: 6
Click here for the answer!
Struggling to finish the quantitative section within the time limit? Learn about GMAT Timing Strategy in our ultimate pacing guide!
Wrapping it All Up
So now you know what topics to expect on the GMAT Math section! A few final words of advice: Know your fundamentals. Don’t try to do everything in your head, but instead write out your scratch work during the test. Lastly, be sure to get in plenty of practice, and learn from your mistakes. Official tests can be found here: Official GMAT Prep Tests 3 and 4.
Good luck on test day!







Leave a Reply