GMAT Probability: Difficult Dice Questions

• Tweet
• Email

• Tweet
• Email

Dice problems aren’t too common on the GMAT. As for the exact probability of getting a dice problem is something only privy to those over at GMAC.

While it is a good idea to know your dice basics, doing so will only help you in the case of an easy dice problem. And one thing is for sure – if you are looking to break a 700 on the GMAT the probability of an easy dice problem (if you end up getting a dice problem) is very, very low.

Below are three excruciatingly difficult dice problems. They will pop up only if you are heading towards a 51Q. For those still brushing up on their math fundamental don’t waste time on such challenge questions.

Practice Questions

1. What is the probability of rolling the same number exactly three times with five six-sided dice?

1. 1/5
2. 5/18
3. 35/216
4. 125/648
5. 225/1296

2. What is the probability of rolling three six-sided dice, and getting a different number on each die?

1. 1/12
2. 1/3
3. 4/9
4. 5/9
5. 7/18

3. A magician holds one six-sided die in his left hand and two in his right. What is the probability the number on the dice in his left hand is greater than the sum of the dice in his right?

1.  7/108
2. 5/54
3. 1/9
4. 2/17
5. 1/4

Explanations:

1. Rolling any number on a dice three times in a row is equal to the number of throws 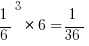, where 3 represents the number of throws and 6 is the number of different ways to get three of the same number (e.g. 1, 1, 1  2, 2, 2  3, 3, 3…).

Next we have to use the combinations formula to determine how many ways three out of five can be the same. 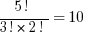. We want to multiply this number to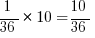

We are not finished yet – there is one little twist to the problem. The question says “exactly three times.” Meaning we have to discount all the instances in which we roll the same number four times and those instance in which we roll the same number five times.

One way to do so is by multiplying by the probability that the fourth and fifth dice will NOT land on the same number as the three dice. Because there are five other possibilities on dice that will not compromise “exactly three numbers” we can multiply by

Finally this gives us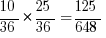

2. For the first die, we can roll any one of six numbers. For the second die, we can roll any number save for the number we rolled on the first die, giving us 5 possibilities. For the third die, we can roll four different numbers (we can’t roll the number we rolled on the first or second die.

6 x 5 x 4 = 120 possibilities out of 216 total possibilities. (For total possibilities we get 6 x 6 x 6 = 216).

120/216 = 5/9

3. Perhaps the hardest of the bunch, this question requires that we find a solution that doesn’t take much longer than 2 minutes. A quick way – or at least relatively quick way – is to determine the number of instances in which our roll of one die will yield more than two die. Intuitively, this is a good place to start because the number of instances in which rolling a great number with one die than with two is much smaller than vice versa.

The only way to roll higher on one die is if the magicians rolls between 2 and 5, inclusive, with two dice. Were he to roll a six with two dice than there is no way he could eclipse that number by rolling one die.

Below is the probability of rolling a certain number with two dice.

‘2’ – 1/36

‘3’ – 2/36

‘4’ – 3/36

‘5’-  4/36

Now the only numbers a magician can roll with the one die and win is between 3 and 6, inclusive. The chances of rolling any are always 1/6.

Next, we have to combine the probability distribution relating to two dice with that relating to the one.

The chances of a magician rolling any given number with one die are 1/6. So let’s start with the lowest number he can roll: a ‘3.’ To win with this roll, he will have to roll a ‘2’ with two dice, the odds of which are 1/36. So .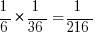

So the chances of him rolling a ‘3’ with one die and winning are 1/216.

Let’s repeat this logic for the next roll, ‘4.’ Chances of rolling are 1/6. Only way a ‘4’ wins is if he rolls a ‘2’ or a ‘3’ with two dice.

Odds of rolling a ‘2’ with two dice  + odds of rolling a ‘3’ with two dice = 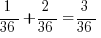. Combine this with the odds of rolling a ‘4’ ( which is 1/6): .

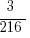If he rolls a ‘5’ with one die, he can win if he rolls a ‘4’ with two dice, the probability is 3/36. He can also win if he rolls a ‘2’ or a ‘3’ with two dice, the number outcomes we just found: 3/36. So we add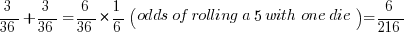

Next, if he rolls a ‘6’ on one die, he can beat ‘2’ through ‘5’ with the two dice. Number of ways to roll a ‘5’ = 4/36. Combining this with the odds of rolling a ‘6’ on one die with the odds or rolling ‘2’, ‘3’, ‘4’, or ‘5’ with the two dice we get: 10/216.

You may be wondering why I left the denominator as 216. Well, this allows us to add up all the instances he can possibly win:

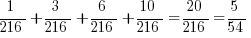 (Answer B)