Logarithms are not incredibly common on the ACT, but you are likely to see one, or maybe two, amongst the harder problems on the ACT Math test, so if you are shooting for a top score on ACT Math, logarithms are worth knowing.
First of all…
What is a Logarithm?
A logarithm is the power to which a number must be raised in order to produce some other number.
If you went, “Huh?” I don’t blame you.
But you probably know about exponents:
If we see 32, we know this is 3 x 3, which equals 9.
If we see 45, we know this is 4 x 4 x 4 x 4 x 4, which equals 1024.
Logarithms are all about thinking about exponents in a different way.
Here’s the question logarithms answer: What is the power something is raised to in order to get a number that we know?
So let’s say we are trying to figure out what power 3 must be raised to to get 9. Well, we just figured that out above: it’s 2. And what if we are trying to figure out what power 4 must be raised to in order to get 1024? Again, we saw this above, it’s 5.
This brings us to the mathematical definition of a logarithm:
Definition of a Logarithm
If logab = c, then ac = b
So you need to remember, “What power do I need to raise a to to get b?
Using our example above, what does log41024 = ______?
Hopefully, you said 5.
Now try this one:
What is log264?
(think to yourself what power do I need to raise 2 to to get 64?)
The answer is 6. 26 = 64.
A Quick Recap
If you find logarithms super-strange looking, you’re definitely not alone! As we’ve seen, we’re used to working with exponents in a format like y = xa. In “logs” that equation is equal to logx(y) = a. Or, looking at an example with actual numbers: 32 = 9 is the equivalent of log3(9) = 2
We would read the logarithm out loud as “log-base 3 of 9 equals 2.” A helpful way to remember this is to notice that whatever is on the other side of the equals sign is the exponent, and that the tiny number is the exponent base.
Change of Base Rule
If you have a scientific or graphing calculator, your calculator has a log button. But this log button only calculates bases of ten (log10). So one more important trick to remember about logs that will help you quickly convert logs of any base to ones you can plug in your calculator is the change of base rule. Here is is:
Logba = log a / log b (a base of 10 is implied when it is not written).
So if you see log48, you can convert this to log 8 / log 4 and plug this in your calculator to get the answer 3/2. Which if you check it back in the problem, it makes sense: 43/2 = 8.
For more info on mastering logarithms, check out the video below!
Logarithm Rules for ACT Math
For your studying ease, here’s a complete list of logarithm rules (most of these will already be familiar to you from your study of exponents).
Practice with ACT Math Logarithms
We can talk about logarithms until we’re blue in the face, but it’s pretty pointless without some practice!
Translate the exponents to logs and the logs to exponents:
Now, solve a few logarithms for the missing info:
As long as you know your exponent rules, you should have no problem with logarithms! The answers to these questions are:
One way to study these is to make flashcards with half of the equation of the front, and the other half on the back. Knowing these by sight will save you time on test day, since you won’t have to convert the logarithms to exponents first to solve.
Try another logarithm question on your own:
You could solve this by following rules for manipulating logorithms: 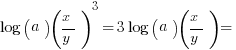
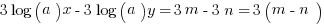


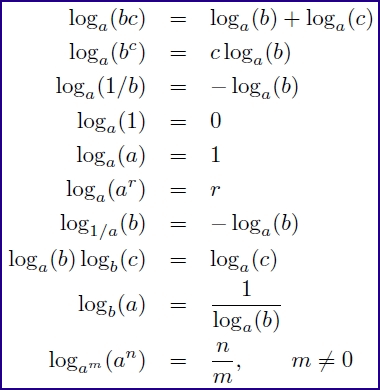
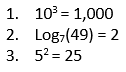
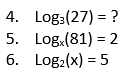
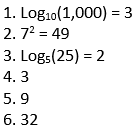
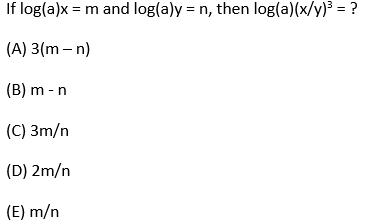
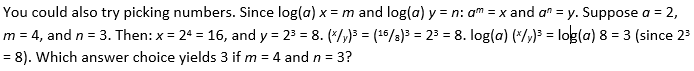
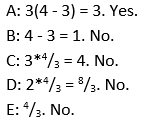




Leave a Reply