Bars and pies? Yum, pass the ice cream! Charts? Whoa, sounds like a fun new board game. Well, in both cases you are mistaken. The most common graphs featured on the SAT math are bar graphs and pie charts. Having a basic understanding of these two graphs can go a long way on the SAT Math Section.
Bar graphs
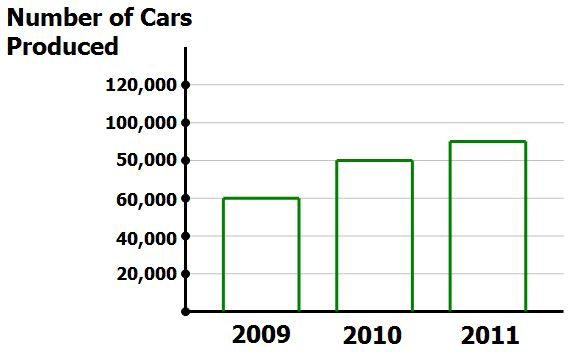
A good way to read these graphs is to first look at the y-axis (the vertical side) and the x-axis (horizontal side). Here you will find information that tells you what the bars about.
In this case, the y-axis represents the number of cars produced. The lowest number is 20,000 and each line represents an increment of 20,000. Sometimes, when the numbers are really big, you’ll have the numbers represented in increments of 20, but in the bottom left hand corner it might say something like “each number is in millions: 20 equals 20,000,000”.
Next, notice the x-axis. Here we have three different years. Each year is represented by a bar. To figure out how many cars were sold in that year, match the top of the graph to the numbers in the y-axis. For instance, in 2009 a total of 60,000 cars were produced.
Sometimes the bar doesn’t exactly touch the line that corresponds to a number in the x-axis (in this case that line is gray and corresponds to each increment of 20,000). For instance, in 2011 the top of the bar is between 80,000 and 100,000. Therefore, 90,000 is a pretty good guess for the number of cars produced in 2011. Don’t worry the SAT is not ridiculous and evil. It won’t say that 2011 is 89,996. The answer spread for how many cars were produced in 2011 would look something more like this:
(A) 50,000
(B) 75,000
(C) 85,000
(D) 90,000
(E) 105,000
Pie charts
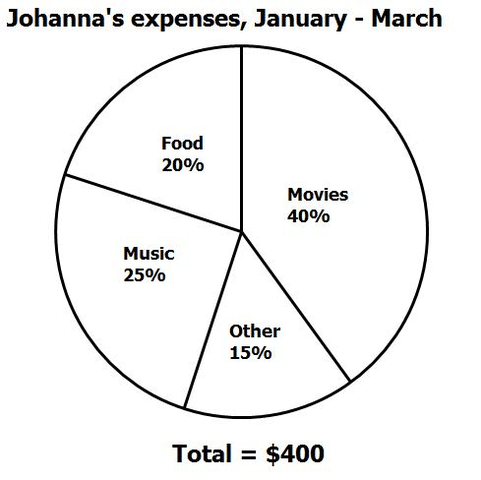
Usually when we cut up pies, we want to make sure each piece is more or less even. In math, pie charts aren’t always even since they are trying to describe the breakdown of different things.
If we look at the pie chart, we can see that the entire pie represents Johanna’s expenses for Jan. to Mar. You’ll notice that Johanna’s expenses aren’t the same. For instance, she really likes going to the movies but apparently isn’t too much into eating (guess she’s not a fan of pie!). To represent this we break up the pie into different percents that each stand for something. In this case we have music, food, movies, and other.
But a percent has to be a percent of something. In this case, that something is $400. So, if the question asked us how much money Johanna spent on food, the answer is 20% of 400, which is $80.
Usually, the SAT will give you something a little more complicated:
5. How much more money did Johanna spend on movies than on music?
To answer this question, we can either find 40% of 400 and 25% of 400 and then subtract those two sums. Or we can see that 40% is 15% more than 25%. 15% of 400 is 60, the answer to the question number 5.
Other graphs
Sometimes, a question might include a combination of a bar and a pie chart. While this might seem pretty scary at first, as long as you understand how each kind of graph works, then you should be fine integrating information from both of them.
There are also other kinds of graphs, such as scatterplots, but those rarely come up, and, when they do, it is only on the hardest-level questions.





