Circles: the odd ducks of the shape world. They have no vertices and they are best friends with a weird number called pi.
You’re probably familiar with the two most commonly used formulas relating to circles — the area and circumference formulas. Just in case, here’s a reminder:
Circumference: C=2πr or dπ, where r is the length of the radius and d is the length of the diameter.
Area: A = πr²
If any of the above terms don’t ring a bell, review the parts of a circle before reading on, because you’ll need to know some circle terms.
All good? Great; let’s forge ahead!
Once you get into coordinate geometry, another equation joins the party; it is known as the Equation of a Circle. I know, shocking.
This equation gives you information about a circle which allows you to map it onto a coordinate plane. It can also help you solve problems that ask about the position of a circle on a graph or in relation to other things, like lines and parabolas.
The equation:
(x – h)² + (y – k)² = r²
The parts:
Alright, so let’s break down what this all means.
The x and y will always be there. They are the variables in this equation.
The point (h,k) is the center of the circle.
The r stands for the length of the radius of the circle.
And that’s it, folks.
How to use it
There are two major uses for this equation: graphing a circle and determining if a given point is on a circle.
Let’s take a look at an example of the former.
Example: (x – 4)² + (y – 3)² = 16
So what can we tell from this? First, the center of the circle is located at (4,3) on the graph. Second, the length of the radius is 4 because the square root of 16 is 4. We could now graph five points on the graph, one at the center, and four at the north, south, east, and west points of the circle by counting five points in each direction. We’ve done that on the graph below, and you can see that both the center of the circle and the radius match up with the numbers we found from the equation. The rest of the circle is sketched in.
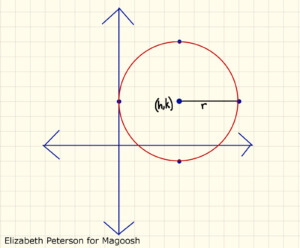
You can also use this equation to test if a given point is on a circle.
Example: Take the point (8, 3), which is graphed above.
If we plug it into the equation for the x and y, we get the following:
(8 – 4)² + (3 – 3)² = 16
4² + 0² = 16
16 = 16
Hooray! The point is indeed on the circle.
Last notes
Of course, there are tricky moments to watch out for. Take the following equation:
(x +2)² + (y + 5)² = 6
Notice that the numbers representing the h and k are being added to the x and y, which actually means they are both negative and the center of the circle is (-2, -5). Also, remember that the radius of the circle is √6, not 6.
As long as you pay attention and keep the template equation in mind, you’ll find the equation of a circle a hugely useful tool for dealing with circles on coordinate planes.






Leave a Reply