Not all averages are created equal on the ACT Math Test. What can be somewhat confusing is that the word “average” on the ACT Math can refer to two separate concepts: the arithmetic mean, and the average speed. It’s important not to confuse the two on the Test Day, as they require different formulas to solve! Here’s what you need to know to tell these two apart!
The “arithmetic mean” is what you’ve probably learned in your high school Algebra class as the mathematical average. This is defined as the sum of the terms divided by the number of terms. Mean = (Sum) / (# of terms). For a list of consecutive integers or evenly spaced numbers, the mean is equal to the median, or the middle number. For example, the “average” of 3, 5, and 9 is 5.67. This is the most-common “average” and the easier of the two concepts.
The concept of “average speed” is often found in complex word problems. This type of question is one many students are less familiar with so you may not have seen it before (and that’s ok). Let’s review two important equations to remember and look at how this concept appears on the tough ACT word problems.
The first formula to memorize is: D = R x T. This stands for Distance = Rate x Time (referred to as the “DIRT” formula). It is perfectly acceptable to also think of it as Time = Distance / Rate or as Rate = Distance / Time as well. Usually the “Rate” is speed but it could be anything “per” anything. In a word problem, if you see the word “per” you know this is a question involving rates.
The second formula is: Average Rate = Total Distance / Total Time. This is its own special concept and you will notice that it is NOT a simple Average of the Speeds (which would be something like the Sum of the Speeds / the Number of Different Speeds or what we know as the Arithmetic Mean). Average Rate is a completely different concept, so do not let the common word “average” confuse you. This concept is extremely rare on the ACT Math section, but it’s nice to know the formula in case it comes up!
Let’s look at a challenging sample question:
The average (arithmetic mean) of four numbers is 30. When one of the numbers is removed, the average of the remaining three numbers is 10. What number was removed?
(A) 30
(B) 45
(C) 60
(D) 75
(E) 90
We know that the four original numbers sum to 30*4 = 120. The new equation becomes:
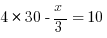
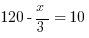
120 – x = 30 (add an x to each side and subtract a 30)
90 = x
The correct answer is (E).




