Because triangles have so many interesting properties that build upon each other, you can count on seeing them on the new SAT. Although the problems that you will encounter won’t necessarily be difficult, the key lies in being able to figure out which property or concept to use in order to get to the answer.
Here you will be tested on figuring out missing side lengths, and you’ll have to brush up on some triangle knowledge before we begin:
- The sum of interior angles in a triangle add up to 180 degrees.
- The Pythagorean Theorem states that the sum of the squares of the two shorter sides of a right triangle equals the square of the longest side (the hypotenuse).
New SAT Math: Similar Triangles
Similar triangles have the same angle measure for all angles, but they don’t necessarily have equal side lengths. All triangles with the same angle measures are similar.
The side lengths of similar triangles are proportional to each other, so we can set up a ratio in order to figure out missing side lengths:
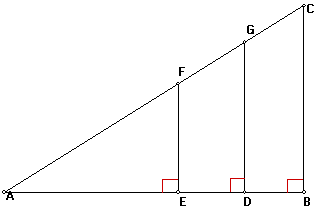
Photo by jwilson
A/E = B/F = C/G
New SAT Math: Congruent Triangles
Congruent triangles are the same size, so they have the same angle measurements and equal side lengths. In other words, they are basically the same triangle.
New SAT Math: Sample Triangle Problem
Let’s take a look at a sample problem:

Triangle ADG (above) has an area of 6 square units. If AD = AF = 3, then what is the length of EF?
A) 12/5
B) 2
C) 8/3
D) 1/2
1. The first thing we want to do here is label our given measurements. Whenever we have a problem that asks us to use or draw a reference picture, we always want to write and draw everything out. Let’s mark down the length of sides AD and AF.
2. Since the area of the entire triangle is given, we can go ahead and solve for the missing side length DG using area = (½)base*height. In this case, we should get
6 = .5*3*height
4 = height
Side length DG is equal to 4.
3. Now we can either use the Pythagorean Theorem to solve for side length AG or see that we have a 3-4-5 right triangle. Either way, we should get 5 for the length of side AG.
4. From here, recognize that since both triangle AEF and ADG share an angle (angle A) and are both right triangles, they must be similar. Therefore, we can set up a ratio between the two triangles in order to solve for length EF.
We will use the two known hypotenuse lengths and the length of DG.
3/5 = x/4
x = 12/5
Our answer here is A!






Leave a Reply