Before we get into the rules, let’s see an example of an SAT question that uses absolute values:
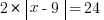
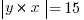
1. In the equations above, x < 0 < y. What is the value of x + y?
(A) -8
(B) -5
(C) 2
(D) 16
(E) 26
Rule 1: Absolute values are grouping symbols
In the question above, there are two ways that we can deal with the first equation.
The first way is to treat the absolute value bars like parentheses. They serve a very similar purpose (the operations inside them have to be carried out before you can do any addition or subtraction), and you can distribute in the same way. So we can figure this:
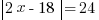
Rule 2: Isolate absolute values
Alright, so maybe you saw the other way to work with that equation. Instead of distributing, you could just divide out the 2 from both sides. It works the same way, in the end.
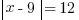
In either case, you’ve done exactly what you need to: get that absolute value alone. Only then can you get rid of the bars.
Rule 3: Make two equations
Getting rid of the bars means splitting the equation into two: one positive equation and one negative. So that first equation ends up like this.
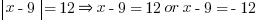
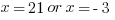
By following the instructions in the question, we know that only one of those is possible.
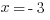
After we plug that in to the second equation, we’ll take away the absolute value bars and, again, split it into two equations.
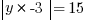
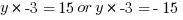
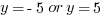
The rest is pretty straight forward. Since y is greater than 0 according to the question, we know y=5, so the answer must be 2, which is (C).
Rule 4: Reverse inequalities for the negative value
If you have an inequality rather than an equation, you still have to split it into two possibilities. But you could also put those two possibilities into one expression. Let’s look at an example of that.
Without any absolute value, the inequality 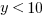 looks like this on a number line:
looks like this on a number line:
But if we put in some absolute value bars, it’ll look different.
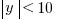
That’s because while y can be -2 or -9, it can’t be -11. If it were -11, the absolute value would be 11, which is too high.
Splitting the inequalities, then, gives you this:
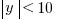
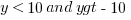
Notice how the direction of the inequality switched when we introduced that negative. The greater a positive number is, the further it is from zero; on the other hand, a lesser negative number is further away.
And if you switch the direction of y > -10 to be -10 < y, it’s pretty clear how we can combine the two possibilities into a single expression that describes the number line we saw.
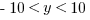
Double check the rules
When you have absolute values on your SAT, always double check what information the question gives you. Does is define whether anything is positive or negative? Then, after you split the equation, be ready to scrap the value which doesn’t work.



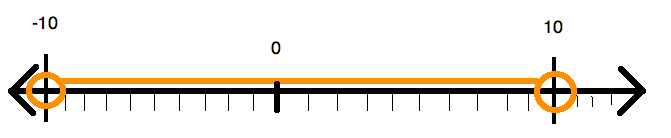




Leave a Reply