Algebra is by far the most important part of SAT math. Isolating a variable is a step in many SAT math problems, depending on whether or not you use elimination strategies. That’s as it should be; after all, you’ve been doing that in math class for the entirety of your high school career, and it’s the foundational block that most other math is built on. It’d be worrying if SAT math didn’t use a lot of algebra.
Of course, that algebra comes in many shapes and forms. Some of it’s relatively basic, while other questions involve so many steps that little slip-ups become a serious threat. One way to make that algebra longer is to include two variables (or more). If you have as many equations as variables, then it’s only a matter of using substitution or combination to get your answer.
You’ve seen at least one of these methods in school, of course, but you may not be equally comfortable with the two. If that’s the case, then take some time getting familiar with the other; you’ll want to have both options to choose from during your SAT.
When substitution is better
If either x or y (or whatever variable you have) stands alone on one side of the equation or can be isolated really quickly, substitution is the way to go. Take a look at the example below.
If 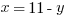 , and
, and 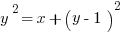 , then what is the value of
, then what is the value of 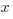 ?
?
This is also ideal for substitution because of the other somewhat complicated stuff going on… if you used combination, you might make a mistake when combining the y terms of the two equations.
So let’s solve it.
First, substitute the x out of the second equation by plugging in the right side of the first equation.
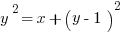
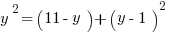
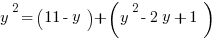
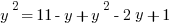
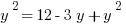
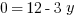
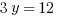
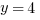
And we’re done, right?
Nope. Almost done.
Remember to check what the question is asking for. In this case it’s the value of x, not y.
But that’s not hard. Just plug that value of y back in to the simpler of the two equations we were given.
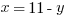
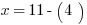
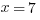
Now it’s done.
When combination is better
If there’s one variable that has the same coefficient in both equations, then combination is probably a good idea. Or better yet, if the coefficient in one equation is the negative of that in the other equation, then we’re set.
What does that mean? Good combination questions look like this:
If 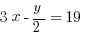 , and
, and 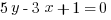 , then what is the value of
, then what is the value of 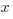 ?
?
With that 3x in one equation and -3x in the other equation, it’s pretty quick to cancel them out. So let’s line up the two equations over each other, then combine them into one.
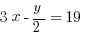
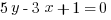
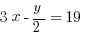
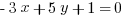
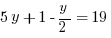
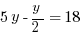
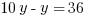
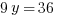
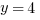
If you fell for that trap the first time, I hope you’re not going to do it again. Find x.
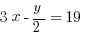
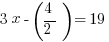
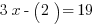
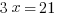
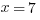
And now we’re done.
Use whichever method is easier on the day of your SAT
While you’re practicing, it’s a good idea to try to vary which method you use, so you have both tools at your disposal. But on the day of your test, you don’t want to spend any time deliberating. Just pick whichever seems easiest and go for it.






Leave a Reply