Quick: how do you find the volume of a cylinder? Do you know the formula?
The SAT will give it to you at the beginning of each math section, along with some other geometric facts, but you should know them anyway. At least, you should be familiar with how you get those formulas.
Start from 2D shapes
The area of a square is 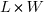 . If you just add in the next dimension, you have the volume of a cube,
. If you just add in the next dimension, you have the volume of a cube, 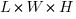 .
.
The same is true for any object that has two congruent 2D shapes at its ends, e.g. a cylinder or a prism. Since a circle’s area is 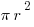 , a cylinder’s volume is that, multiplied by the other dimension.
, a cylinder’s volume is that, multiplied by the other dimension. 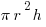 .
.
If you’re trying to find the distance between two points in a figure, start with the two dimensional shapes—the faces of the object—and find whatever measurements you can from there. And of course you should draw in any extra lines that the figure doesn’t show. They, too, will be possible to work with as pieces of 2D shapes, like triangles. They’re easier to deal with.
Remember the meaning of words describing 3D shapes
Some questions prey on students who mix up vertexes, edges, and sides (or faces). Don’t fall for the SAT’s tricks! A side is a two dimensional shape. If you rolled the object on the ground, it could possibly stand on a side.
Compare that to an edge, which is where two sides meet. It’s one-dimensional. Think of the edge of a knife to help remember the word. A cube (like a die) rolled on the ground is pretty much never going to land on an edge.
And a vertex is a single point with no dimensions. It’s just another word for “corner.” The tip of a cone is a vertex, for example.
Just another geometry problem
Most 3D shapes aren’t much more difficult to deal with than their two dimensional counterparts, at least not mathematically. Visualizing can be a little bit tricky, it’s true, but don’t freak out if you see a 3D shape. Take it one dimension at a time.






Leave a Reply