About a quarter of SAT math problems need some geometry skills to be solved, and most of those ask you to use geometry knowledge alone. So you could say that getting all of the geometry questions right would earn you about 150 points on the test, although if you’re wondering how to calculate SAT scores), it’s really not that simple.
Those SAT geometry questions are mostly about three topics: triangles, circles, and angles. When students ponder the typical question, “how hard is SAT math“, terrible visions of shape monsters often appear in their heads.
Triangles (and angles) in SAT geometry
The most important of those three is definitely triangles. The SAT loves triangles. So much, in fact, that half of the reference information they give you at the beginning of each math section is about the measurements of triangles.
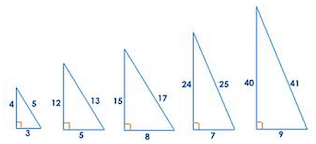
Specifically, the SAT uses a lot of right triangles in questions. You’ll get plenty of chances to use the Pythagorean theorem. If that sounds dull, then make it easier by knowing some Pythagorean triples ahead of time. Here are a few:
The smaller the triples are, the more common they are on the SAT (so 3-4-5 triangles are the most common). Of course, they show up as their multiples pretty often too; instead of a 3-4-5, you might see a 6-8-10 triangle. If you have two sides of a right triangle that match up to any of the ones above, then you know the third side even without using the Pythagorean theorem.
The special right triangles they give you in the reference info are also among the SAT’s favorites. Recognize and know the proportions of 30˚-60˚-90˚ and 45˚-45˚-90˚ triangles and you’ll save yourself time and energy both.
You might not even see a triangle at first. A lot of times, the question doesn’t ask you specifically about a triangle, but if you add a bit of info to the figure (or draw your own figure), you’ll see a triangle appear. And more often than not it’s going to be a right triangle.
Circles in SAT geometry
Circles don’t just appear like triangles do. They’ll be given to you specifically, so when you see the word circle, a picture of one, or a picture of a piece of a circle (like an arc), then you should be pretty clear on where to start.
Take a quick look at the formulas for circle measurements.
Diameter = 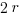
Circumference = 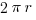
Area = 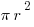
Volume of a cylinder = 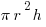
What do you see in common? Before you do anything else, check if you can find the radius of a circle on the SAT. It’s probably going to help you along to the answer.
Also, it’s good to remember a couple other things about the radius:
- Any two radii of one circle are equal in length
- A line tangent to the circle is perpendicular to a radius line
Using circles and triangles on the SAT
There are a lot of problems that aren’t as simple as “What is the length of side XY?” or “What is the area of circle O?” on the SAT.
In fact, you’ll need to combine those skills on several SAT questions. Be ready to move information around, and always remember to write in any information that’s not given to you in the figure. If tables and charts are more your fright, check out SAT Charts for more help there.






Leave a Reply