SAT math loves number properties almost as much as it loves triangles. Of course, that’s actually a wide range of topics. Number properties describe how integers can be broken down, combined, or worked with in different ways; exponent patterns, odds and evens, positives and negatives, and divisibility all fall under the number property umbrella, as do others.
Getting these question right on your SAT comes down to a few things. The most important is simply knowing rules (e.g. negative times negative is positive). Beyond that, you also have to be capable of finding patterns in numbers. Doing a little bit of experimenting and looking for rhyme or reason pays off. You also have to see numbers inside numbers.
That is, if you see a 21, you should immediately recognize that’s 7 times 3 and be ready to work with that fact. Questions that ask about factors and multiples are perfect examples of how the SAT assesses that skill.
Splitting integers up
You’re probably already pretty familiar with factor trees, so I’m not going to bore you with how to make one. But just in case you’re a little fuzzy on what it looks like:
…such a comfortable, familiar shape. I learned how to draw a Christmas tree like that when I was in kindergarten and I’ve been doing it ever since. (Clearly, I am quite the artist.)
By the way, you should remember that those factors hanging off of the very bottom of our tree are all prime numbers.
Least Common Multiple
Though the SAT rarely uses the terms, you should definitely be comfortable finding both least common multiples and the greatest common factors before you take the test.
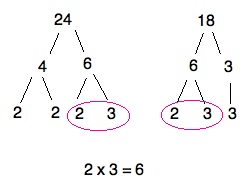
The LCM is the smallest number that includes all of the prime factors of both numbers.
Sometimes that means just multiplying all of the numbers together if the two numbers don’t share any common factors.
Sometimes it means taking just as many as you need.
Since 4 gave us 2 as a factor twice, we don’t need to use the 2 from the factors of 6.
Greatest Common Factor
The greatest common factor is pretty similar. Get the prime factors of both numbers, then find what’s in common. Sometimes there’s nothing shared, like with 9 and 4 above, which means the GCF is 1 (both are divisible by 1, after all). Sometimes there’s only one factor in common, like with 6 and 4 above. In that case, the GCF is 2, since that’s the only factor they share.
But sometimes, you need to multiply together shared factors.
If you want to be extra careful, you can always divide both number by that GCF you got.
All of the factors
Sometimes you’ll need to find all of the factors of a specific number. That means making a factor tree, then combining those prime factors in every possible way.
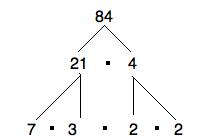
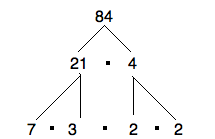
Lets use that factor tree for the number 84.
Those prime factors are a start. Also, remember that every list of factors should start with the number 1, since it’s a factor of every integer.
So our list so far is 1, 2, 3, and 7.
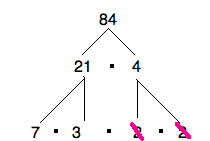
Now, let’s combine them. Let’s start with the 2 furthest on the right, and combine it with every other prime factor.
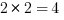
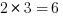
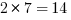
So we can add 4, 6, and 14 to the list.
Now let’s combine that 2 with pairs of the other prime factors.
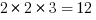
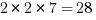
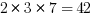
Add 12, 28, and 42 to the list….
Then we’re done using the first 2, so cross it off.
Keep going with the next factor. Using the other 2 is pointless though…
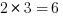
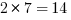
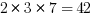
We’ve seen those before, so we’ll move on.
Now we can combine 3 and 7.
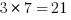
So we add 21 to the list.
After that, the only piece left is the largest factor of all: 84.
Our list is now 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.
If you have to get all the factors of a number, do it systematically. Don’t just start listing whatever you can think of—you’re bound to miss one that way. And never forget 1 and the number itself.

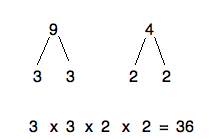

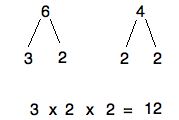





Leave a Reply