New SAT Math Standard Deviation

Standard deviation is now a concept that tested on the new SAT Math for the Problem Solving and Data Analysis question types. If you’re completely unfamiliar with standard deviation, you’ve come to the right place! Here’s all you need to know to about standard deviation and how to ace new SAT Math standard deviation questions.

What is Standard Deviation?

Standard deviation is a statistical measurement of variation in a data set, or how far or how close the data as a whole is to the mean. Standard deviation is always measured in the units of the data set.

If a data set has a small standard deviation, it means that data as a whole is closer to the mean. In other words, data with a small standard deviation has little variation, or differences, in the data.

On the other hand, if a data set has a large standard deviation, it means that the data is further away from the mean. Data with a large standard deviation has more variation in the data.

Standard Deviation in Action

Typically, groups that are pretty similar have smaller standard deviations and groups that are more diverse have larger. For example, say we are looking at the heights of thousands of Americans. Within that population, we also looked at the heights for only basketball players.

Chances are the standard deviation for all Americans would be larger–meaning there are more differences in height within Americans–than the standard deviation for basketball players–meaning that the heights of basketball players are more similar.

Shaq and Bush- New SAT math standard deviation - Magoosh — Similar as in they’re *all* reaaalllyyyy tall

Standard deviation can get a lot more complicated than this. For example, if you were to take a statistics class, you’d probably need to learn how to use the formula that calculates standard deviation.

Here’s the thing about SAT Math though:

You only need to know about the basic idea of standard deviation and how it’s used to compare two data points for new SAT Math standard deviation problems.

New SAT Math Standard Deviation Sample Question

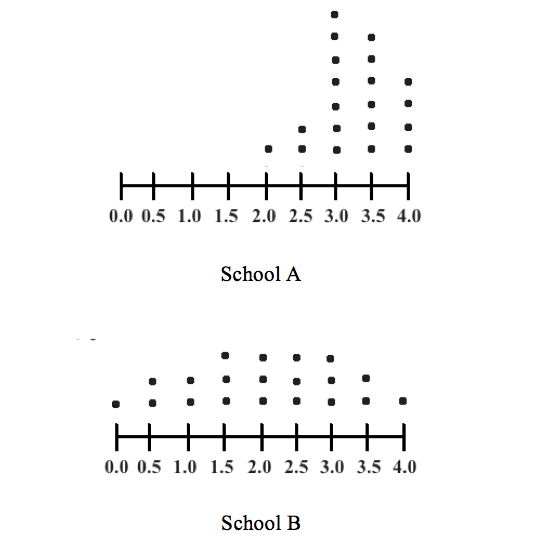
The dot plots above indicate senior GPAs at two schools in the same district, School A and School B. Each dot represents 5 students and each school has 100 seniors. Which of the following correctly compares the standard deviation of the scores in each of the classes?

(A) The standard deviation of the GPAs in School A is smaller.
(B) The standard deviation of the GPAs in School B is smaller.
(C) The standard deviation of the GPAs in School A and School B is the same.
(D) The relationship cannot be determined from the information given.

Hint: If you’re struggling with how to start with this problem, look at the spread of data for both data sets. Which one has a bigger data spread? A smaller data spread? And how does this correspond to a big or small standard deviation?

How to solve this question

When you’re asked to compare the standard deviations of two data sets, there’s a two-step process that you should follow:

Make an educated guess about the mean of each data set by locating its center.
Analyze each data set to see if it has points that are closely grouped around the mean or more spread out from the mean.

Just by eyeballing the dot plot for School A, it would appear that the center and mean of the data set would be between 3.0 and 3.5. For School B, the center and mean seem to be right at 2.0.

For School A, we can see that most of the points seem to be grouped around 3.0 and 3.5, which would correspond to a smaller standard deviation. School B clearly has its data much more spread out, so it’s safe to say that School B has a larger standard deviation. Therefore, (A) is the correct answer here.

Remember:

The key to succeeding on new SAT Math standard deviation questions is by remembering that a smaller data spread always means smaller standard deviation while a bigger data spread means bigger standard deviation. But make sure you don’t let outliers fool you into thinking a data set has a big spread of data. For example, what if the above data plots looked like this instead?

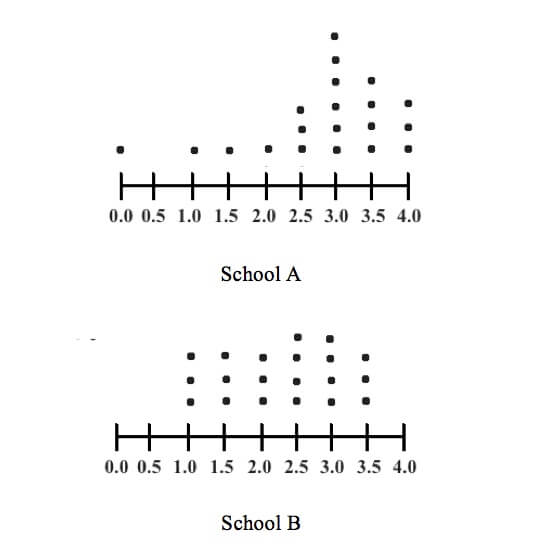
Although School A now looks like it has a bigger spread than school B because it has a larger range, School A still has more values clustering around the higher end of the plot while School B still has an even spread of data across more GPA values.

Need more help?

With Magoosh ACT, you can choose between a live cohorted class with an instructor (which includes all our lessons and practice questions) or access to the self-study option by itself.

Author

Anika Manzoor

As one of Magoosh’s Blog Editors, Anika relies on her nearly 20 years in education and youth leadership spaces to produce empowering, student-centered content across Magoosh’s blogs. Anika has a BA from Grinnell College and an MPP from Harvard University. Her experience includes serving two years as a Fulbright English Teaching Assistant in Malaysia, an SAT tutor for Kaplan, and currently, as the Executive Director of Youth Activism Project, a nonprofit that she co-founded when she was 12 years old. Anika’s work has been featured in The Washington Post, The Boston Globe, and Yahoo! Money. She has also spoken at panels and given presentations at New York University and Harvard University. If you’d like to keep up with Anika, you can check out her LinkedIn, Instagram, Twitter, and personal website.

View all posts