
Photo by wecometolearn
Quadratic equations giving you trouble on the SAT? Check out this post for all you need to know about solving quadratic equations on the new SAT math.
Solving Quadratic Equations on the New SAT Math: The Basics
Quadratic equations consist of a variable raised to the power of 2 as the highest-powered term. On a graph, they usually produce a “U” shape.
The standard form of a quadratic equation is ax2 + bx + c = 0. We always want to set the equation equal to 0 so that we can find out what x is when y = 0.
Because they contain multiple solutions, quadratic equations are a bit more involved than linear equations. Quadratics have either 0, 1, or 2 real solutions – you will generally not need to find the imaginary solutions.
There are a few common ways to say “find the solution” to a quadratic problem:
- Find the root.
- Find the x-intercept.
- Find the zeros.
Solving Quadratic Equations on the New SAT Math: Use Algebra
Multiplying Binomials
Remember FOIL? They stand for First, Outer, Inner, and Last. It’s a handy acronym for remembering how to distribute everything correctly.
(a + b)(c + d) = ac + ad + bc + bd
From here, you’ll usually need to simplify a couple of terms in order to get it to look like one of the answer choices on the test.
Factoring
This is basically the opposite of FOIL. You are trying to figure out what two binomials, when multiplied together, equal the expression. Remember to set the entire equation given equal to 0 first before starting on factoring.
This method works best when you have a 1 for the coefficient of your quadratic variable (x2). We just need to find out what our b and d is to create (a + b)(c + d).
Let’s take a look back at ax2 + bx + c.
The first way to narrow down your options is to think about what two numbers multiply together to equal the value of the constant c. Once you’ve written out the possible options, figure out which pair of numbers, when added together, equal the coefficient of the variable raised to the power of 1.
Now you can solve for x! All you have to do is set x equal to whatever will make each binomial 0.
Once you are good at this, you will be able to get to the answer more quickly and not have to think about every single possible choice when guessing numbers.
Completing the Square
This method is a bit more involved but is usually faster than using the quadratic equation. Note that you can only use this option if the coefficient of the variable raised to the power of 1 is an even number.
Let’s try solving x2 – 2x – 1 = 0.
1. The first step is to move the constant over to the right side. This gives us
x2 – 2x = 1
2. Next, figure out what binomial, when multiplied by itself, matches the left side of the equation.
(x – 1)2 = 1
3. Since (x – 1)2 gives us x2 – 2x + 1 on the left side, we need to add that 1 to the right side as well.
(x – 1)2 = 2
4. Square root both sides and solve for x.
x = 2.41 and x = -0.41
Solving Quadratic Equations on the New SAT Math: Use a Calculator
With your graphing calculator, you can just punch the numbers in and see where the graph intersects with the x-axis. Make sure you enter in the numbers correctly so that you don’t get a weird answer.
The best way to save time while doing this is to plug everything into the calculator, and then move on to the next question while waiting for the calculator to load so that you don’t lose precious time.
Solving Quadratic Equations on the New SAT Math: Use the Quadratic Formula
If you’re really stuck and nothing’s working out for you, you can try using the quadratic formula. Here it is in all its glory:
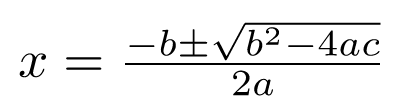
It’s not a super difficult process, but it can eat up a lot time to list out the equation and plug in the numbers. This route should only be considered as a last resort.






Leave a Reply