
Click here for the first part of this series: the basics of Heart of Algebra on the New SAT.
In order to do even rudimentary algebra, you’ll need to understand how to combine like terms and, if the question asks to solve for a variable, how to isolate that variable. Below is a quick review to help you with these basics. If you think you understand them, then try the slightly more difficult question that comes at the end.
Combining like Terms
In order to combine two or more terms, every term must have the same variable and the same power next to that variable. By “combining”, I mean adding or subtracting terms.
Here is an example of terms that cannot be combined:
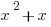
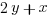
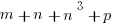
Here is an example of terms that can be combined (and I’ve gone ahead and done just that!)
Similar variables:
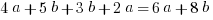
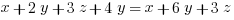
Similar exponents (will need to know for Passport to Advanced Math):
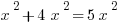
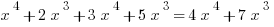
Solving Equations
#1 –
Isolate the variable
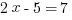
In this equation, we want to make sure x is by itself. To do this, we want to make sure all the numbers are on one side of the equal side and the variable, assuming there is one variable, is on the other side of the equal side.
#2 –
What you can do to one side of the equation, you have to do to the other side.
We want to make sure that the equation always remains the same. Therefore, we can’t add or subtract something to one side of the equation without doing the same thing to the other side of the equation. Since we want to get rid of the number on the left hand side, or at least “move” it to the other side, we have to add 5 to both sides, giving us the following:
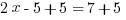
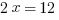
Now we divide both sides by 2 so that we can “isolate” the x:
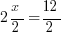
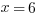
Here’s a practice question of the type that you can expect from the Heart of Algebra section:
Practice Question
1) Which of the following correctly simplifies the expression 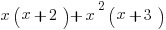 ?
?
A) 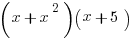
B) 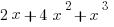
C) 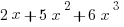
D) 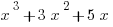
Explanation
First we want to multiply the expression out, giving us
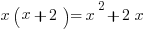
And
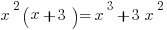
Giving us
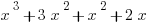
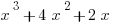
Answer B.
The ability to quickly work through equations like this will help you a great deal on test day.






Leave a Reply