Below is a list of formulas and math facts you’ll need if you’re looking to ace SAT math. A lot of it should be old hat for you at this point—after all, you study this stuff in school, right?—but it’s definitely handy to have it all in one place for reference, and there are some nifty shortcuts sprinkled through the list that you might not be aware of yet, too.
For more detailed information about the math formulas you’ll need to know for the SAT, be sure to take a look at Magoosh’s SAT Math Formula eBook! (And for even more free SAT prep, you can check out Magoosh’s SAT study guide, as well!)
Arithmetic and Number Properties
Order of Operations
The Associative Property:
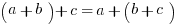
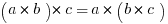
The Distributive Property:
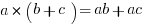
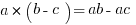
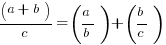
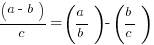
Fast Fractions
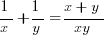
For example: 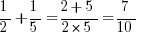
Exponents and Roots
Laws for Combining:
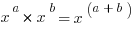
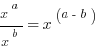
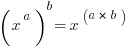
1 and 0 as bases:
- 1 raised to any power is 1. 0 raised to any nonzero power is 0
- Any nonzero number to the power of 0 is 1, e.g.

Fractions as exponents:
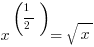
Negative exponents:
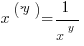
Negative bases:
- With an even exponent: positive result
- With an odd exponent: negative result
Roots
Estimating roots:
To estimate square roots of numbers that aren’t perfect squares, just examine the nearby perfect squares. For example, to find 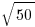 , you know that
, you know that 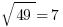 and
and 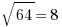 , so find
, so find 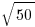 must be between 7 and 8.
must be between 7 and 8.
Cube roots:
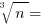 a number that, when cubed, equals n. E.g.:
a number that, when cubed, equals n. E.g.:
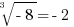
Simplifying roots:
Separate the number into its prime factors, and take out matching pairs. E.g.:
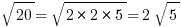
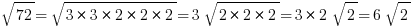
Adding roots:
Roots can be added like variables. E.g.:
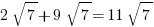
Prime Numbers and Integers
- 1 is not a prime.
- 2 is the smallest prime and the only even prime.
- An integer is any counting number including negative numbers (e.g. -3, -1, 2, 7…but not 2.5)
Ratios
Ratios let us compare the proportions of two quantities.
If there is a 2:5 ratio of boys to girls at a school, that means that for every 5 girls, there are 2 boys. So there could be 2 boys and 5 girls, 20 boys and 50 girls, 200 boys and 500 girls, etc.
Ratios are given by x:y, x to y, or x/y. If a question says “for every x there is/are a y,” you are most likely dealing with a ratio question. Ratios can also be x:y:z.
Ratios can be simplified like fractions. 3:6 is the same as 1:2.
Remember that if there is a 2:5 ratio of boys to girls at a school, the ratio of boys to total students is 2:(5 + 2) = 2:7. So 2/7 of the students are boys.
Percentages
The Meaning of “Percent”
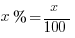
Calculating Percentages
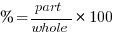
Percent Change
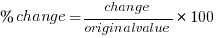
Divisibility
3 : sum of digits divisible by 3
4 : the last two digits of number are divisible by 4
5 : the last digit is either a 5 or zero
6 : even number and sum of digits is divisible by 3
8 : if the last three digits are divisible by 8
9: sum of digits is divisible by 9
Algebra
FOIL
First, Outer, Inner, Last:
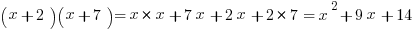
Common patterns to memorize:
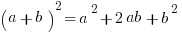
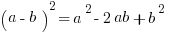
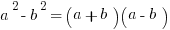
Cross-Multiplication
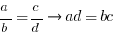
Quadratic equations:
For 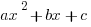 , where a is not 0, if you can factor it to
, where a is not 0, if you can factor it to 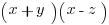 , then the solutions are -y and z. For example:
, then the solutions are -y and z. For example:
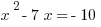
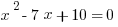
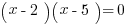
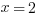 or
or 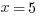
Geometry
Angles
A right angle is made up of 90 degrees
A straight line is made up of 180 degrees.
If two lines intersect, the sum of the resulting four angles equals 360
Circles
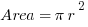
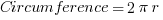
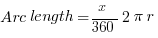
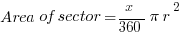
Triangles
General:
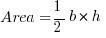
Side A – Side B < Side C
Side A + Side B > Side C
Right Triangles:
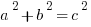 where c is the hypotenuse.
where c is the hypotenuse.
A 45˚-45˚-90˚ triangle has sides in a ratio of x : x : x√2, with x√2 as the hypotenuse
A 30˚-60˚-90˚ triangle has sides in a ratio of x : x√3 : 2x, with the 1x side opposite the 30 degree angle and 2x as the hypotenuse
Certain right triangles have sides with all integer lengths. These sets of numbers are called Pythagorean triples, and you should memorize some of them: 3-4-5, 5-12-13, and 8-15-17. A multiple of a Pythagorean triple is also a Pythagorean triple (e.g., 6-8-10).
Squares
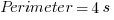 , where s = side
, where s = side
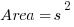
Rectangles
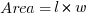 , where l = length and w = width
, where l = length and w = width
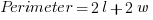
Trapezoids
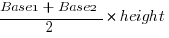
Polygons
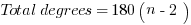 , where n = # of sides
, where n = # of sides
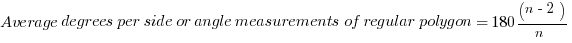
Coordinate Geometry
Slope-Intercept Form
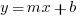 , where m is the slope and b is the y-intercept.
, where m is the slope and b is the y-intercept.
Slope
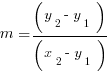
The Distance Formula
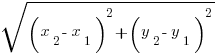
Word Problems
Sequences
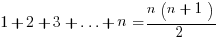
Probability
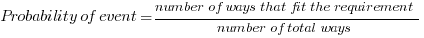
Averages
Mean:
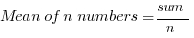
Median:
The middlemost value when numbers are arranged in ascending order; for an even count of numbers, take the average of the middle two
Mode:
The number that occurs most frequently in a list or set
Distance, Rate, and Time
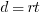 ,
, 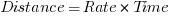
Counting
Combination:
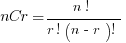
When the order does not matter—for example, picking any 3 friends from a group of 5.
Permutation:
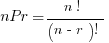
When the order does matter—for example, how many ways you could order 3 letters from the word PARTY?

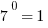





Leave a Reply