Interval Notation

In mathematics we mostly want to be as efficient and precise as possible when describing certain principles, and one such example is interval notation. An interval of real numbers between a and b with a < b is a set containing all the real numbers from a specified starting point a to a specified ending point b.

Interval Notation: The Types of Intervals

There are a few different types of intervals that commonly arise when studying math, called the open interval and the closed interval, notated respectively as (a, b) and [a, b].

Interval Notation for Open Intervals

The open interval uses parentheses, and they signify the fact that the interval contains all the real numbers x that are strictly between the numbers a and b, i.e. the interval does NOT actually contain the numbers a and b. Another way of notating an open interval is the set of all x such that a < x < b.

Interval Notation for Closed Intervals

In the case of the closed interval, the square brackets are used to indicate that the endpoints are contained in the interval. Therefore we can notate a closed interval as the set of x so that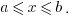

Interval Notation for Half-Open Intervals

There are slightly fancier intervals, called half-open intervals, notated as (a, b] and [a, b), which are the respective sets of all x so that , and .

An interval is called bounded when there is a real positive number M with the property that for any point x inside of the interval, we have that |x| < M.

Observations on Intervals

Supposing as in the setup that a < b, then how many numbers are actually in the interval (a, b)? It turns out that there are uncountably infinite numbers in any interval (a, b) where a < b, no matter how close a and b are together.

It is a fact that actually, there are the same quantity of real numbers in the interval (0, 1) as there are in the entire real numbers, also represented by the interval . This seems counterintuitive, because one interval seems so much more vast than the other, but it is not a contradiction, but rather a beautiful subtly of set theory.

Calculus and Intervals

Intervals arise regularly in calculus, and it will be important for you to know the difference between a closed interval and an open interval, since there are some theorems, like the intermediate value theorem, which requires that the interval upon which the function is defined is a closed and bounded interval.

Closed and bounded intervals touch on one of the most important concepts in the broader study of calculus, that of compactness. Many central theories in calculus revolve around compact sets, which in the setting of the real numbers are exactly the closed bounded intervals.